Podstawy automatyki

Rozdz. 18. Charakterystyka amplitudowo-fazowa 

Rozdz. 18.1 Wstęp
W sposób najbardziej naturalny poznasz pojęcie charakterystyki amplitudowo – fazowej. Na wejście układu członu dynamicznego podamy sinusoidy o częstotliwościach od 0 do nieskończoności, a praktycznie od bardzo małej do konkretnej dużej. Sinusoida wyjściowa będzie miała tę samą częstotliwość, ale inną amplitudę (przeważnie mniejszą) i inną fazę (przeważnie opóźnioną) niż wejściowa. Wyznaczona w ten sposób amplituda i faza układu otwartego dla całego zakresu częstotliwości zawiera w sobie łatwą do odczytania informację o stabilności układu zamkniętego.
Charakterystykę częstotliwościową układu otwartego wyznacza się stosunkowo łatwo. Możesz to zrobić „na żywca” nawet  obiekcie bez obaw, że stracisz panowanie nad instalacją przemysłową. Jest to przecież układ otwarty, a więc stabilny.
Jeżeli znasz liczby zespolone, to wykreślisz charakterystykę amplitudowo-fazową podstawiając s=jω do G(s) i rysując na płaszczyźnie zespolonej kolejne wartości wyrażenia  G(jω) dla różnych pulsacji ω.

Rozdz. 18.2 Wirujący wektor  jako model przebiegów sinusoidalnych
Cosinusoidy i sinusoidy często występują w automatyce, elektrotechnice, akustyce…
Rozdz. 18.2.1 Wirujący wektor jako cosinusoida 1cos(ωt).
 Zaczniemy od cosinusoidy.

Rys.18-1
Rys. 18-1a
Cosinusoida x(t)=1cos(ωt) dla ω=1/sek jako ruch harmoniczny na osi x. 
Rys. 18-1b
Ruch obrotowy cosinusowego wektora jedynkowego 
Wektor o długości 1 ma stan początkowy [1,0]=1+j0 i obraca się z prędkością obrotową ω=+1/sek (czyli z okresem T=2π sek i przeciw zegarowo).  Opisany jest zespolonym   równaniem z=1*exp(jωt)*
A teraz najważniejsze! Rzut końca wektora jedynkowego na oś x na to nic innego jak animacja na Rys. 18-2a!
Rys. 18-1c
Wykres x(t)=1cos(ωt)
Powyższe 3 rysunki opisują ruch harmoniczny x(t)=1cos(ωt), czyli dokładnie to samo zjawisko. Ale wersja wirującego wektora jako z=1*exp(jωt) jest najbardziej intuicyjnym modelem funkcji cosinus. Tu najlepiej są widoczne amplitudy A i przesunięcia fazowe φ! *Proponuję rozdział Funkcja zespolona exp(jωt) jako wirujący wektor w artykule “Wirujące Szeregi Fouriera” w górnej zakładce rozdział 3.1 . Jeżeli jesteś mniej biegły w liczbach i funkcjach zespolonych to rzuć jeszcze okiem na artykuł “Liczby Zespolone”. 
Rozdz. 18.2.2 Wirujący wektor opóźnionej cosinusoidy 1cos(ωt-90º) jako sinusoida 1sin(ωt).

Rys. 18-2
Rys. 18-2a
Sinusoida x(t)=1sin(ωt) dla ω=1/sek jako ruch harmoniczny na osi x. 
Rys. 18-2b
Ruch obrotowy sinusowego wektora jedynkowego
Wektor ma stan początkowy [0,-1] inaczej 0 -1j=-1j i obraca się z prędkością obrotową ω=1/sek (czyli z okresem T=2π sek.
Opisany jest równaniem  z=-1j*exp(jωt) lub inaczej  z=1*exp(jωt-90º)
Rzut końca wektora porusza się na osi x na Rys. 18-3a zgodnie z równaniem x(t)=1sin(ωt).
Rys. 18-2c
Wykres x(t)=1sin(ωt)=1cos(ωt-90º)
To wszystko opisuje ruch harmoniczny x(t)=1sin(ωt). Zauważ, że opóźnienie φ=-90º sinusoidy  1sin(ωt) względem cosinusoidy 1cos(ωt) jest najlepiej widoczne na wirujących wektorach Rys. 18-2b i Rys. 18-1b.
Rozdz. 18.2.3 Wirujący wektor opóźnionej cosinusoidy 1cos(ωt-45º)

Rys.18-3
Rys. 18-3a
Cosinusoida x(t)=1cos(ωt-45º) dla ω=1/sek jako ruch harmoniczny na osi x. 
Rys. 18-3b
Ruch obrotowy wektora jedynkowego dla x(t)=1cos(ωt-45º)
Wektor ma stan początkowy [1/√2,-1/√2] inaczej 1/√2,-1j/√2 i obraca się z prędkością obrotową ω=1/sek (czyli z okresem T=2π sek.  Opisany jest równaniem  z=(-1/√2,-1j/√2)*exp(jωt). Można go opisać inaczej i chyba prościej z=1*exp(jωt-45º)
Rzut końca wektora porusza się na osi x na Rys. 18-3a zgodnie z równaniem x(t)=1(ωt-45º).
Rys. 18-3c
x(t)=1cos(ωt-45º)
Rozdz.18.2.4 Dwa wirujące wektory 1cos(ωt) i 0.75cos(ωt-45º) czyli o różnej amplitudzie i fazie
Z wektorami o różnej amplitudzie i fazie spotkamy się w rozdz. 18.5 i następnych.

Rys. 18-4
Rys. 18-4a
Wirujący wektor z=1exp(jωt)
Rys. 18-4b
Wirujący wektor z=0.75exp(jωt-30º)
Rys. 18-4c
2 funkcje 1cos(ωt) i 0.75cos(ωt-30º)
Wniosek
Na  wektorach lepiej widać amplitudy  i opóźnienie ϕ=-30º cosinusoid niż na wykresie. Pamiętaj też o tym, że dla pełnej informacji przy wektorach musi być podana pulsacja – tu ω=1/sek!

Rozdz. 18.3 Wyznaczanie charakterystyki amplitudowo-fazowej członu proporcjonalnego
Zaczniemy od najprostszego członu. czyli proporcjonalnego.

Rys. 18-5
Charakterystyka amiltudowo-fazowa członu Proporcjonalnego
Dla tego członu G(s)=1 w każdej chwili jest x(t)=y(t). Czyli sinusoida wyjściowa y(t) jest równa sinusoidzie wejściowej x(t) dla każdej pulsacji ω. Dlatego charakterystyka amplitudowo-fazowa jest tak prosta, że aż trudna. Sprowadza się do jednego punktu (+1,0).

Rozdz. 18.4 Wyznaczanie charakterystyki amplitudowo-fazowej członu inercyjnego
Rozdz. 18.4.1 Wstęp
Do tej pory stosowaliśmy głównie analizę czasową członów dynamicznych. Dawaliśmy jako wejście x(t) skok jednostkowy, impuls Diraca lub piłę. Wtedy odpowiedź y(t) była informacją o własnościach dynamicznych tego członu. Zależy mi na tym, żeby czytelnik kojarzył parametry transmitancji G(s) z odpowiednimi charakterystykami czasowymi. Do tego przyda się oczywiście znajomość liczb zespolonych, ale nie jest to absolutnie konieczne. Wspomniałem tylko, że s z G(s) jest liczbą zespoloną i żeby się tym za bardzo nie przejmować. Dlatego nie pojawiło się dotychczas jedno z najbardziej podstawowych pojęć w automatyce:
Charakterystyka Amplitudowo-Fazowa
Jest ona rozszerzeniem pojęcia-pasmo przenoszenia.  Na wejście dajemy sinusoidę której częstotliwość powoli zmienia się teoretycznie od zera do nieskończoności a praktycznie to tylko np. 30 częstotliwości od bardzo małej do dużej.
Odpowiedzią y(t) też jest sinusoida o tej samej częstotliwości, ale o innej amplitudzie i fazie.
Te wielkości tj. amplituda i faza dla różnych ω, pokazane na jednym wykresie wskazowym (np. Rys. 18-5) tworzą charakterystykę amplitudowo-fazową. W odróżnieniu od pasma przenoszenia zawiera ona także informację o fazie sygnału.
Wyznaczymy teraz charakterystykę amplitudowo-fazową dla członu inercyjnego o parametrach:
K=1
T=1 sek
Zaczniemy od bardzo małej pulsacji ω=0.31 1/sek (T=20 sek!) a skończymy na ω=10.06 1/sek (T=0.63 sek). Zielona sinusoida wejściowa x(t) ma zawsze stałą amplitudę Xm=1. Dla każdej pulsacji wyznaczymy amplitudę Ym i fazę φ czerwonego sygnału wyjściowego y(t) w postaci wektorowej.
Rozdz. 18.4.2 ω=0.31/sek (T=20 sek)

Rys. 18-6
Wejściem jest sinusoida x(t) o amplitudzie Xm=1 i ω=0.31/sek (T=20 sek)
Sinusoida wyjściowa ma amplitudę Ym=0.95 i opóźnienie φ=-17.5°. Krótko i na temat –  Czerwona sinusoida y(t) jest opóźniona o φ=-17.5° względem zielonej  x(t). Przedstawiono też te same sinusoidy jako wektory. Dużo lepiej jest tu widoczna faza i amplituda czerwonej sinusoidy y(t). Parametry Ym i φ wyznaczamy możliwie najpóźniej (tu po ok. 25 sek).  Wtedy sinusoida jest już „uspokojona”. Na samym początku mamy stan przejściowy, w którym sinusoida y(t) z „kolankiem” tak naprawdę nie jest jeszcze sinusoidą. Jak się później przekonasz, stany przejściowe są wyraźniejsze przy większych częstotliwościach.
Rozdz. 18.3.3 ω=0.63/sek (T=10 sek)

Rys.18-7
Wejściem jest sinusoida x(t) o amplitudzie Xm=1 i ω=0.63/sek (T=10 sek)
Opóźnienie y(t) zwiększyło się na φ=-32° i amplituda zmniejszyła  y(t) na Ym=0.85.
Z wykresu w pierwszej chwili wydaje się, że takie same ω jak poprzednio. Ale zmieniła się podstawa czasu!
Tu i w następnych doświadczeniach eksperyment trwa 30 sek a nie 60 sek jak poprzednio.
Rozdz. 18.3.4 ω=1.26/sek (T=5 sek)

Rys. 18-8
Xm=1 i ω=1.26/sek (T=5 sek)
Opóźnienie y(t) zwiększyło się na φ=-52° i amplituda zmniejszyła  y(t) na Ym=0.61
Rozdz. 18.3.5 ω=2.51/sek (T=2.5 sek)

Rys. 18-9
Xm=1 i ω=2.51/sek (T=2.5sek)
Opóźnienie y(t) zwiększyło się na φ=-68° i amplituda zmniejszyła  y(t) na Ym=0.37
Rozdz. 18.3.6 ω=5.03/sek (T=1.25 sek)

Rys. 18-10
Czerwona strzałka y(t) dalej się opóźnia i zmniejsza. Przy większych częstotliwościach wyraźniej widać stan przejściowy sinusoidy na początku przebiegu.
Rozdz. 18.3.6 ω=10.06/sek (T=0.63 sek)

Rys. 18-11
Jak zwykle czerwona strzałka dalej się opóźnia i zmniejsza. Przypuszczamy, że dla bardzo dużej częstotliwości amplituda będzie dążyła do 0 a faza do -90°. Wyraźnie tu widać na początku stan przejściowy czerwonej sinusoidy wyjściowej y(t)
Na tym kończymy pierwszy etap wyznaczania charakterystyki amplitudowo-fazowej  członu inercyjnego 1/(1+sT).
Rozdz. 18.4.7 Charakterystyka amplitudowo-fazowa badanego członu inercyjnego
Zróbmy z kolejnych wykresów wskazowych (strzałek) jeden wspólny rysunek.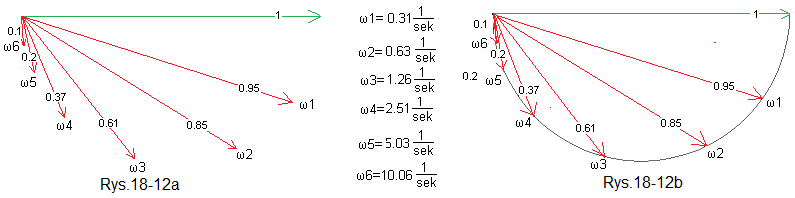

Rys. 18-12
Wspólnym rysunkiem jest Rys. 18-12a. Zielony wektor to symbol 6 sinusoidalnych sygnałów wejściowych x(t) o pulsacjach ω1, ω2, ω3, ω4, ω5, ω6 i amplitudzie Xm=1. Pozostałe 6 czerwonych wektorów, to odpowiednie odpowiedzi sinusoidalne. Tu było tylko 6 pulsacji. A gdyby było ich więcej np. sto, albo idźmy na całość-milion? Otrzymamy wtedy Rys. 18-2b w którym koniec wektora kreśli półokrąg.
Rzuć jeszcze okiem na następny rysunek.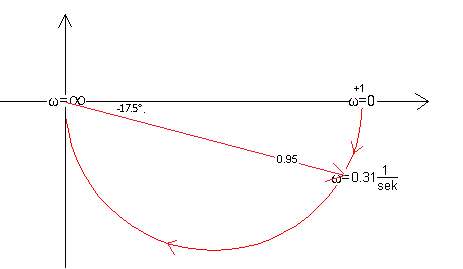

Rys. 18-13
Końce wszystkich wektorów widoczne są jako czerwony półokrąg. Dodano osie x,y. Niby podobny, ale jak traktować czerwony wektor odpowiedzi na sygnał sinusoidalny wejściowy x(t) o pulsacji ω0=0?
Po pierwsze nie robiliśmy takiego eksperymentu, a po drugie to czym jest zerowa pulsacja lub częstotliwość? Traktuj ją jako baaardzo małą pulsację! Np odpowiadającą okresowi T=1 rok. Cały rok siedzisz przed oscyloskopem i obserwujesz sinusoidę. Startujesz 1 stycznia z poziomu x(t)=0. Po pierwszym kwartale masz sygnał x(t)=+1 itd. Zgodzisz się z tym że y(t) też będzie powolne i z prawie zerowym przesunięciem φ. Tak małym, że możesz przyjąć φ=0. Amplituda też będzie 1.
Zauważ, że nie mamy zielonego wektora x(t). Był on tylko potrzebny ze względów dydaktycznych. Mało tego, nawet czerwone wektory są niepotrzebne. Tu zachowaliśmy tylko jednego ich przedstawiciela dla pulsacji ω=0.31/sek. Wystarczy sam półokrąg jako końce różnych wektorów.
Charakterystyka amplitudowo-fazowa jest uogólnieniem pojęcia pasmo przenoszenia ( to z kolei jest uogólnieniem pojęcia wzmocnienie). Można z niej odczytać nie tylko wzmocnienie dla danej pulsacji ale także fazę.Tu np. widać że dla ω=0.31/sek wzmocnienie K=0.95 i przesunięcie fazowe φ=-17.5°.
Każdy człon inercyjny ze wzmocnieniem K=1 startuje z pulsacją ω=0 z punktu (+1,0) i kończy w ω=nieskończoność w punkcie (0,0).
Gdyby stała czasowa T była 2 razy większa czyli G(s)=1(1+2s), to wtedy dla  ω=0.31/sek byłoby K=0.85 i φ=-32°.
Dla innego wzmocnienia, np. dla K=3 początek byłby (+3,0) ale koniec taki sam–>też (0,0). Półokrąg byłby 3 razy większy.

Rozdz. 18.5 Wyznaczanie charakterystyki amplitudowo-fazowej członu całkującego
Rozdz. 18.5.1 Człon całkujący jako przykład astatycznego
Człon inercyjny i proporcjonalny są tzw. członami statycznymi. Widać w nich początek dla ω=0 i koniec dla ω=∞. A jak jest dla członu astatycznego np. całkującego to za chwilę sam się przekonasz. Będziemy badać człon całkujący podobnie jak poprzednio  człon inercyjny.
Rozdz. 18.5.2 ω=0.31/sek (T=20 sek)

Rys.18-14
Sinusoida wyjściowa y(t) ma amplitudę 3.2 oraz przesunięcie fazowe φ=-90°. Obok przedstawiono jej wykres wektorowy który przedstawia to samo. Czerwony wektor wyjścia  y(t) o długości 3.2 też jest opóźniony o φ=-90° względem wejścia x(t).
Rozdz. 18.5.2 ω=1.25/sek (T=10 sek)

Rys. 18-15
Amplituda zmniejszyła się dwukrotnie na 1.6, za to faza φ=-90° pozostała taka sama.
Rozdz. 18.5.3 ω=1.26/sek (T=5 sek)

Rys. 18-16
Amplituda zmniejszyła się dwukrotnie na 0.8, φ=-90°.
Rozdz. 18.5.4 ω=2.51 1/sek (T=2.5 sek)

Rys. 18-17
Amplituda zmniejszyła się dwukrotnie na 0.4, φ=-90°.
Rozdz. 18.4.5 ω=5.03/sek (T=1.25 sek)

Rys. 18-18
Amplituda zmniejszyła się dwukrotnie na 0.2, φ=-90°.
Rozdz. 18.4.6 Charakterystyka amplitudowo-fazowa członu całkującego
Zróbmy z Rys.18-14…Rys. 18-18 jeden wspólny rysunek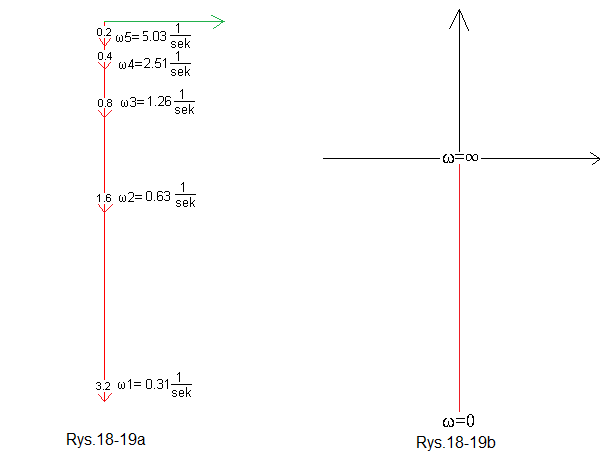

Rys. 18-19
Tym wspólnym jest Rys.18-19a.
Rys. 18-19b przedstawia zaś charakterystykę amplitudowo-fazową członu całkującego, bez strzałek i dla wszystkich 0<ω<∞. Dla ω=0 moduł wzmocnienie członu całkującego to K=∞ a dla ω=∞ to K=0.

Rozdz. 18.5 Człony statyczne
Nie mają elementów całkujących. Czyli nie mają pojedynczych s-ów w mianowniku G(s). W odpowiedzi na skok dają stan ustalony, a nie rosną do nieskończoności jak astatyczne. Może to być człon przedstawiony wcześniej inercyjny a także wieloinercyjny, oscylacyjny, z opóźnieniem itd… Ich charakterystyki jako bardziej złożone niż inercyjny, nie są już półokręgami, aczkolwiek czymś podobnym. Człon trójinercyjny daje np. taką charakterystykę”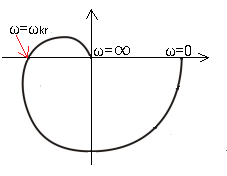

Rys. 18-20
Charakterystyka członu trójinercyjnego przechodzi przez trzy ćwiartki. Można się domyślać, że dwuinercyjny to tylko dwie ćwiartki, tak jak biedaczysko inercyjny ma tylko jedną. Dla pewnej pulsacji ω=ωkr sinusoida wyjściowa y(t) członu trójinercyjnego jest w przeciwfazie do sinusoidy wejściowej x(t) Czegoś takiego nie ma człon dwuinercyjny (bo jest tylko w 2 ćwiartkach), ani tym bardziej inercyjny.

Rozdz. 18.6 Wnioski
Wcześniej traktowaliśmy transmitancję G(s):
-Intuicyjnie jako “coś”, co przekształca sygnał wejściowy x(t)  sygnał wyjściowy y(t). I tak np. człon inercyjny G(s)=2/(1+3s) przekształca skok jednostkowy x(t)=1(t) na przebieg wykładniczy y(t) dążący do y=2 ze stałą czasową 3T. Czyli G(s) kojarzyłeś z odpowiedzią na skok jednostkowy.
-Ściśle jako iloraz G(s)=Y(s)/X(s)  gdzie Y(s) jest transformatą Laplace’a y(t) zaś X(s) jest transformatą Laplace’a x(t)
Można powiedzieć, że obie definicje się uzupełniają bo:
–intuicyjna nie jest ścisłą
–ścisła nie jest intuicyjną
Teraz transmitancja G(s) przekształca każdą sinusoidę x(t)=1sin(ωt)  o pulsacji ω=0…∞ w sinusoidę y(t)=Asin(ωt-φ) o amplitudzie A i przesunięciu fazowym -φ. Przykładem jest  Rys.18-13. Tu człon inercyjny G(s)=1/(1+1s) zamienia sinusoidę wejściową  x(t)=1sin(ωt) dla ω=0.31/sek, w sinusoidę wyjściową y(t)=sin(ωt-φ) gdzie A=0.95 i -φ=-17.5º. Każdy punkt charakterystyki amplitudowo-fazowej odpowiada pulsacji ω=0…∞, z którego można odczytać amplitudę i fazę sinusoidy wyjściowej y(t)=Asin(ωt-φ). Krótko mówiąc, transmitancja G(s) jest charakterystyką amplitudową fazową. Zawiera informację jak przekształcać każdą sinusoidę wejściową x(t)=1sin(ωt) w zakresie ω=0…∞  w sinusoidę wyjściową y(t)=sin(ωt-φ). Jest uogólnieniem pasma przenoszenia, w którym jest nie tylko wzmocnienie K dla każdej częstotliwości, ale także przesunięciu fazowe -φ.
Zauważ, że definicja G(s) jako charakterystyka amplitudowo-fazowa jest w miarę ścisła i intuicyjna.