Podstawy automatyki

Rozdz. 12 Całkowanie

Rozdz. 12.1 Wstęp
Są całki nieoznaczone i oznaczone.

Rozdz. 12.2 Całka nieoznaczona F(t) z funkcji f(t)
Całka nieoznaczona z funkcji f(t) jest tzw. funkcją pierwotną F(t) i często nazywa się po prostu całką.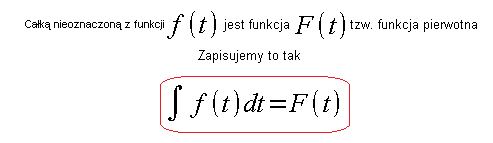

Rys. 12-1
Pochodną funkcji pierwotnej F(t) jest sama funkcja f(t) i odwrotnie – całką nieoznaczoną z funkcji f(t) jest funkcją pierwotną F(t).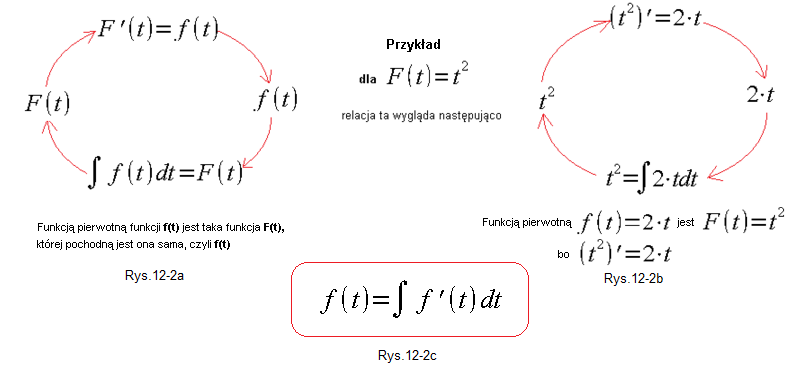

Rys. 12-2
Całkowanie i Różniczkowanie są działaniami wzajemnie odwrotnymi. Całkowanie jako obliczanie funkcji pierwotnej F(t) jest pewną biegłością, którą nabierają studenci pierwszego roku politechnik i inne niehumany. Potrzebna jest do obliczania tzw. całek oznaczonych. Będą one omówione za chwilę. Zwykle na wyższych latach pamięta się tylko najprostsze całki inaczej funkcje pierwotne . Jest to słuszne podejście, bo zawsze można wrócić do notatek z wykładów.
W krótkich żołnierskich słowach. Funkcja pierwotna z pochodnej funkcji jest właśnie tą funkcją (Rys. 16-2c).

Rozdz. 12.3 Całka oznaczona z funkcji x(t)
Rozdz. 12.3.1 Wstęp
W automatyce mamy bardziej do czynienia z całką oznaczoną niż nieoznaczoną. Ta ostatnia jako funkcja pierwotna służy do bardzo łatwego obliczania wartości całki oznaczonej.
Rozdz. 12.3.2 Całka oznaczona z funkcji x(t) jako pole pod funkcją x(t)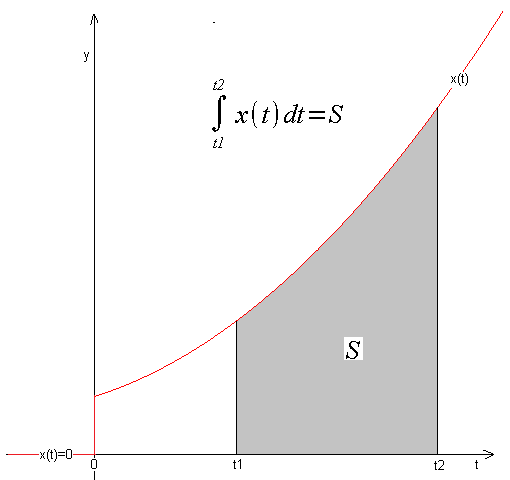

Rys. 12-3
Całka oznaczoną od t1 do t2 jest pole S pod funkcją x(t). Jest to więc konkretna liczba np. S=27.13. Dla naszych potrzeb nieco zawęzimy tę definicję. W automatyce zwykle coś zaczyna się w czasie t=0 i trwa do czasu t. Np. sygnał wejściowy x(t) może być skokiem jednostkowym albo piłą. Przyjmuje się więc, że że dla t<0 (ujemnego!) sygnał x(t)=0.–>Rys. 12-3.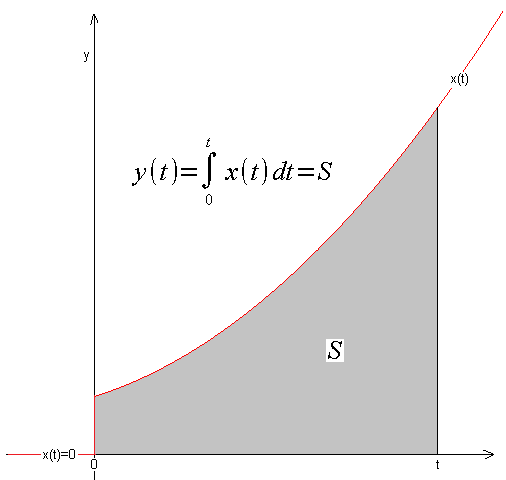

Rys. 12-4
Jest to więc wersja z Rys. 12-3 której t1=0 i t2=t. Przy takim podejściu całka oznaczona staje się funkcją y(t) a nie konkretną liczbą.
A teraz najważniejsze. Jak obliczamy pola na Rys. 12-3 i Rys. 12-4. A no tak.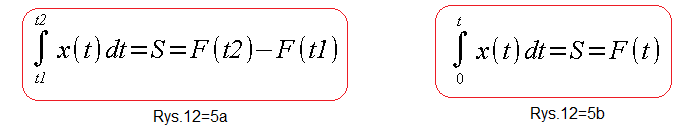

Rys. 12-5
F(t1) i F(t2) na Rys. 12-2a to wartości funkcji pierwotnych, czyli całek nieoznaczonych dla t1 i t2.
Samo F(t1) możemy traktować też jako pole na lewo od t1 i analogicznie F(t2) jako pole na lewo od t2. Przy takim podejściu wzór z Rys. 12-2a jako różnica pól jest oczywisty.
A na Rys. 12-2b już samo F(t) jest po prostu funkcją pierwotną! W następnych 2 doświadczeniach sprawdzimy czy tak jest. Czy teoria zgadza się z praktyką?
Rozdz. 12.3.3 Całka oznaczona z funkcji która jest skokiem jednostkowym x(t)=1(t)
Dlaczego akurat skok jednostkowy x(t)=1(t)? Bo już nie ma prostszej funkcji i łatwo z niej wyliczyć całkę oznaczoną = pole S.
Potraktujmy całkę oznaczoną jako wyjście y(t) członu całkującego którego wejściem jest x(t)=1(t). Okaże się że y(t)=t(t).

Rys. 12-6
Wejściem członu całkującego jest skok jednostkowy x(t)=1(t) a jego wyjściem jest całka y(t)=t(t)
Przypominam, że:
1(t)=0 dla t<0 i 1(t)=1 dla t>0
t(t)=0 dla t<0 i t(t)=t dla t>0 czyli t(t) jest tzw. piłą
Całka oznaczona od 0 do t dowolnej funkcji, jest polem pod wykresem tej funkcji.
Tu x(t)=1(t) jest bardzo proste i łatwo liczy się pole pod funkcją jako pole prostokąta o bokach h=1 i t. Dla dowolnego t>0 pole y(t)=t(t)=t.
Np. dla t=5 y(t)=5. Czyli teoria zgadza się z praktyką.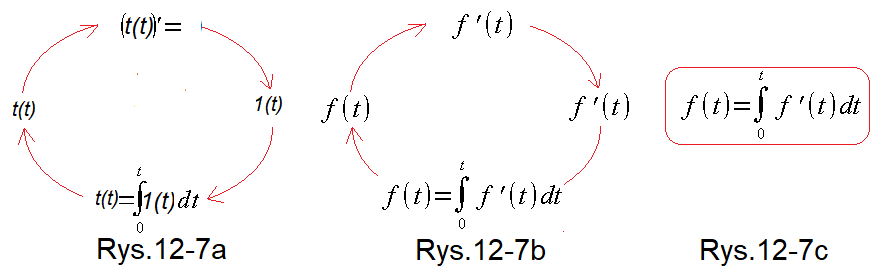

Rys. 12-7
Czyli w skrócie “pochodna z całki oznaczonej w zakresie 0…t jest funkcją podcałkową.
Rys. 12-7a
[t(t)]’=1(t)  czyli pochodna z całki jest funkcją podcałkową
Rys. 12-7b
Uogólnienie poprzedniego
Zamiast funkcji t(t) jest po prostu ogólna f(t)
Rys. 12-7c
Ostatecznie
Całka oznaczona z pochodnej czyli f'(t) jest funkcja f(t)Czyli różniczkowanie jest odwrotne do całkowania.
Rozdz. 12.3.4 Całka oznaczona z funkcji która jest piłą x(t)=0.2*t
Dla piły da się wyliczyć całkę oznaczoną jako pole trójkąta. Sprawdzimy więc, czy wyjście z członu całkującego jest całką oznaczoną.

Rys. 12-8
Wejściem członu całkującego jest „piła”, inaczej sygnał narastający liniowo, tu wg wzoru x(t)=0.2*t.
Całkę oznaczoną z x(t) obliczymy jako pole trójkąta o podstawie t i wysokości x(t)=0.2*t.
Tu np. dla t=9sek piła x(t)=0.2*9=1.8 i pole trójkąta S=0.1t²=8.1
Teoria zgadza się z praktyką. Sygnał za członem całkującym jest parabolą o podanym wzorze i dla np. t=9 sygnał wyjściowy y(t)=8.1.
Rozdz. 12.3.5 Całka oznaczona z funkcji którą jest “machanie suwakiem”. Inaczej sterowanie ręczne typu I
Całka oznaczona jest zawsze polem pod funkcją od czasu t=0 do czasu t.
Nawet gdy funkcja jest bardziej skomplikowana tak jak poniżej. Całka może być dodatnia, zerowa lub ujemna.

Rys. 12-9
Zaobserwuj sygnał wyjściowy y(t) w zależności od zmieniającego się położenia suwaka x(t).
Przekonasz się że:
 – Im bardziej dodatnie x(t) tym szybciej narasta y(t)
– Im bardziej ujemne x(t) tym szybciej maleje y(t)
– x(t)=0 to zatrzymanie y(t) na ostatnim poziomie.
To utwierdza nas w przekonaniu, że x(t)=y'(t). Mówiąc nieprecyzyjnie za to trafnie „x(t) jest pochodną całki” lub „kólka z Rys. 16-8 są prawdziwe”.
W moim doświadczeniu 52 sekundzie gdy y(t)=0 wtedy pole dodatnie x(t) równe jest polu ujemnemu (pole liczone do t=52 sek.)

Rozdz. 12.4 Podsumowanie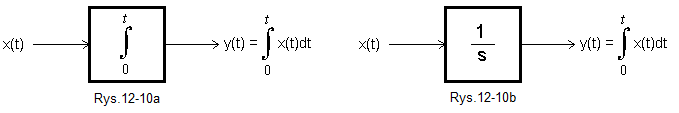

Rys. 12-10
Symbole członu całkującego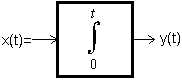

Rys. 12-11
Wyjście y(t) jest całką wejścia x(t)
lub Wejście x(t) jest pochodną wyjścia y(t).