Podstawy automatyki

Rozdz. 7 Człon oscylacyjny

Rozdz. 7.1 Wstęp

Rys. 7-1
Człon oscylacyjny i poznany wcześniej człon dwuinercyjny są przykładami transmitancji G(s) w której licznik jest liczbą stałą d, a mianownik dwumianem drugiego stopnia o parametrach a, b, c–>Rys. 11-1a.
Na Rys. 7-1b parametry a,b,c,d mają konkretne wartości 8,2,2,4.
Z postaci ogólnej Rys. 7-1 nie widać wyraźnie, czy jest to jest to człon dwuinercyjny czy oscylacyjny.
Dlatego należy G(s) z Rys. 7-1a przekształcić do postaci znormalizowanej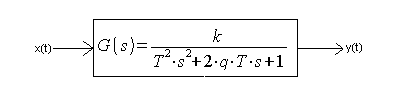

Rys. 7-2
Człon oscylacyjny-postać znormalizowana.
A w niej:
k – wzmocnienie w stanie ustalonym
q – współczynnik tłumienia-im większy tym silniejsze tłumienie oscylacji
T – współczynnik okresu oscylacji. Podkreślam tylko. Współczynnik T, nie sam okres oscylacji Tosc.
Teoretyczny okres oscylacji obliczymy wg wzoru Tosc=2*Π*T. W dodatku jest to wzór przybliżony. Prawdziwy okres oscylacji na wykresie będzie dokładny tylko dla tłumienia q=0. Tłumienie q zwiększa ten okres.
Znormalizowane G(s) cudaczne trochę, ale wszystko będzie jasne po zbadaniu konkretnej transmitancji G(s) z Rys. 7-1b.
Na początek sprowadźmy ją do postaci znormalizowanej, czyli takiej jak na Rys. 7-2.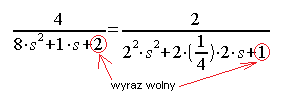

Rys. 7-3
A jak to zrobić?
1 Podziel licznik i mianownik przez 2, tak by w mianowniku wyraz wolny (czyli bez s) stał się 1
2 … itd
Oczywiście L=P i sprawdź to.
W ten sposób otrzymamy po prawej stronie postać znormalizowaną. Wynika z niej, że k=2, T=2 sek (czyli Tosc=2*Π*T=12.56 sek) i q=0.25. W następnych punktach będziemy badać tę transmitancję i jej modyfikacje przy różnych tłumieniach q.
Uwaga
Z wartości współczynnika tłumienia  q wynika:
q=0–> idealny człon oscylacyjny – bez tłumienia –>Rozdz. 7.5
0<q<1 rzeczywisty człon oscylacyjny – z tłumieniem–>Rozdz. 7.2 , 7.3 ,7.4 , 7.6
q>=1 człon dwuinercyjny–>Rozdz. 7.7
Czas na laboratorium!

Rozdz. 7.2 k=2 T=2 sek q=0.25 z suwakiem i bargrafem
Zaczynamy od suwaka i bargrafu. Co prawda trudno jest odczytać parametry oscylacji obserwując bargraf, za to poczujesz ten ciężarek na sprężynie. Przyda się na zabawie w remizie.

Rys. 7-4
Pobaw się tym ciężarkiem. Proponuję dać wymuszenie skokowe suwakiem na ok. +0.4. Zobaczysz oscylacje. Poczekaj trochę, aż się uspokoi i oblicz wzmocnienie k używając w stanie ustalonym mierników cyfrowych. Powinno być k=2. Z parametrami T i q na razie dajmy sobie spokój. Wrócimy do nich używając oscyloskopu.

Rozdz. 7.3 k=2 T=2 sek q=0.25 ze skokiem i oscyloskopem
Jaki będzie prawdziwy okres oscylacji Tosc z wykresu w porównaniu do teoretycznego Tosc=12.56 sek obliczonego obliczonego pod Rys. 7-3?

Rys. 7-5
Wzmocnienie k=2 idealnie zgadza się z teorią.
Prawdziwy okres oscylacji Tosc=13 sek na oscyloskopie jest trochę większy od teoretycznego Tosc=12.56 sek*.
A tłumienie q? Też można obliczyć ten parametr z wykresu, ale darujmy sobie. Wystarczy nam wiedza, że q zwiększa Tosc oraz powoduje szybsze zanikanie drgań. Przekonamy się o tym w następnych doświadczeniach.
*Tosc=2*Π*T=12.56 sek

Rozdz. 7.4 k=2 T=2 sek q=0.125 ze skokiem i oscyloskopem
Jak dwukrotne zmniejszenie tłumienia do q=0.125 wpłynie na przebiegi?

Rys. 7-6
Oscylacje trwają dłużej. i nawet nie zdążyły się uspokoić do 60 sekundy.
Okres oscylacji zmniejszył się do Tosc=12.9 sek ale nadal jest większy od idealnego Tosc=12.56 sek.
Wzmocnienie k=2 jest oczywiste. Zwiększyła się także pierwsza amplituda.
A gdyby tak całkowicie pozbyć się tłumienia dając q=0?

Rozdz. 7.5 Idealny człon oscylacyjny k=2 T=2 sek q=0 ze skokiem i oscyloskopem
Jak brak tłumienia, czyli q=0 wpłynie na przebiegi?

Rys. 7-7
Co jest grane? Nie ma stanu ustalonego y(t)=2. Zamiast niego jest składowa stała 2 wokół której „lata” sinusoida o amplitudzie też 2. I tak to będzie do końca świata. Zauważ że prawdziwe Tosc=12.56 sek z wykresu i jest równe teoretycznemu. Jest to cecha idealnego członu oscylacyjnego.
Do tej pory zmniejszaliśmy tłumienie, aż doszliśmy do idealnego oscylacyjnego gdzie q=0. To pójdźmy teraz w drugą stronę z tłumieniem i zwiększmy je na q=0.5.

Rozdz. 7.6 k=2 T=2 sek q=0.5 ze skokiem i oscyloskopem

Rys. 7-8
Odpowiedź y(t) tak jakby zbliżyła się do dwuinercyjnej, chociaż jest to jeszcze człon oscylacyjny. Amplituda zmalała i Tosc=14.8 sek wzrosło. Najbardziej odbiega teraz od teoretycznego 12.56 sek. Idźmy więc na całość i dajmy q>1 np q=1.5.

Rozdz. 7.7 Człon „oscylacyjny” k=2 T=2 sek q=1.5 ze skokiem i oscyloskopem
Nazwa „oscylacyjny” w cudzysłowie i dwuinercyjny w nazwie pliku coś sugerują. Za chwilę się wyjaśni.

Rys. 7-9
No właśnie. Typowa odpowiedź członu dwuinercyjnego. Okazuje się, że dla q>1 człon oscylacyjny staje się dwuinercyjnym!. Stąd też cudzysłów w tytule rozdz.7.7. Skoro jest to dwuinercyjny to da się sprowadzić transmitancję z Rys. 7-9 do postaci z Rys. 6-1 z poprzedniego rozdz.6.

Rozdz.7.8 Człon „oscylacyjny k=2 T=2 sek q=0.25 z dirakiem i oscyloskopem

Rys. 7-10
Dirac pokazuje to, co najciekawsze w członie oscylacyjnym– tylko składową zmienną. Tosc=13 sek jest takie samo jak na Rys. 7-5. Wzmocnienie k jest już trudniejsze do obliczenia, acz możliwe.

Rozdz. 7-9 Cztery z dirakiem i oscyloskopem jednocześnie
Jako posumowanie damy jednoczesny impuls diraka na 4 człony dynamiczne z różnymi tłumieniami q. Wszystkie mają T=0.5 sek i k=1 Jako x(t) wybraliśmy diraka. Wtedy odpowiedź nie ma składowej stałej i łatwiej jest zaobserwować wpływ tłumienia q na przebiegi czasowe.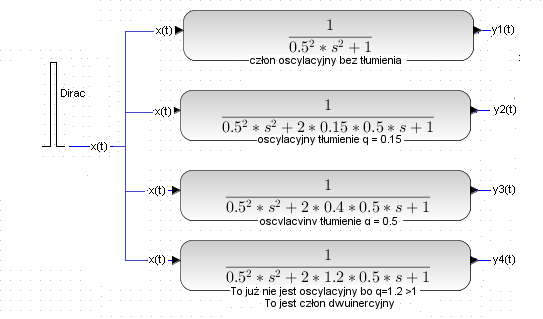

Rys. 7-11
Ten sam krótki ale mocny sygnał x(t) podawany jest na wejścia kolejnych członów o zmniejszającym się współczynniku tłumienia q.
To krótkie x(t) “uderzenie młotka” jest przybliżeniem idealnego impulsu Diraca.

Rys. 7-12
Widać wyraźny wpływ tłumienia q. Im większe tłumienie, tym mniejsze skłonność do oscylacji.
Dla największego q=1.2 nie ma już nawet oscylacji. człon oscylacyjny stał się dwuinercyjnym

Rozdz. 7.10 Wnioski
1. Transmitancja członu oscylacyjnego dla 0 <q<1 przedstawia Rys. 7-2.
2. Dla q=0 jest to człon oscylacyjny idealny w którym drgania nigdy nie gasną.
3. Ze wzrostem tłumienia q maleją oscylacje. Zwiększa się także okres oscylacji Tosc.
4. Dla q>=1 mamy do czynienia z członem dwuinercyjnym. Wtedy mianownik G(s) można przedstawić tak jak na Rys. 6-1 w rozdz. 6

O transmitancji członu oscylacyjnego i dwuinercyjnego można też powiedzieć inaczej

Rys. 7-13
To samo można wyrazić używając tzw. liczb zespolonych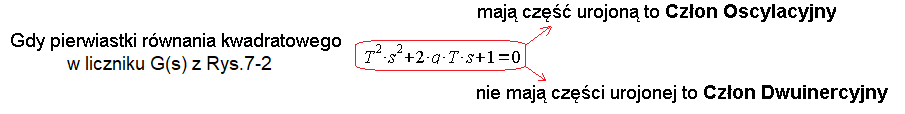

Rys. 7-14 Znajomość liczb zespolonych nie jest konieczna, ale jeżeli chcesz coś więcej to kliknij Kursy w nagłówku i wybierz kurs Liczby Zespolone.