Podstawy automatyki

Rozdz. 1 Wstęp 

Jeżeli chcesz wiedzieć jak działa regulator, w tym król regulatorów – PID, to ten kurs jest dla Ciebie! Zwłaszcza jeżeli nie czujesz się pewnie w świecie całek i pochodnych. Będziesz samodzielnie badał różne obiekty w czasie rzeczywistym! Ważne, że będą to przebiegi o “zwykłym” czasie trwania -przeważnie w zakresie 10 …120 sek. Widać jak wszystko się rusza i pełza! Nie tak gdy przebieg trwa tylko 30 µs, lub w drugą stronę 30 lat. To także zupełnie co innego, niż wykresy czasowe w książkach, np. dotyczące członu inercyjnego. Czyli w dużym uproszczeniu, obserwowanie wzrostu temperatury pieca, gdy na grzałkę podam skokowo (“nagle”) napięcie 230V. Zauważysz, że prędkość wzrostu temperatury (a nie sama temperatura!) jest największa na początku, potem stopniowo maleje. W końcu temperatura zatrzyma się np. na 300°C. Gdy doświadczenie powtórzę z połową poprzedniej mocy, to przebieg będzie podobny, ale zamiast 300°C będzie 150°C.
Człon inercyjny jako model pieca jest bardzo uproszczony. Przebieg czasowy prawdziwego pieca będzie trochę inny. Np. początkowa prędkość wzrostu temperatury jest zerowa. Także w połowie mocy będzie np. 170°C. a nie 150°C. Ale to już zupełnie inna historia..
W kursie jest mało rzeczy na “słowo honoru”. Staramy się wszystko sprawdzić.
Na przykład. Sprawdzamy w/g kryterium Hurwitza czy dany obiekt G(s) jest stabilny, a potem prztykając wejście impulsikiem x(t), próbujemy wytrącić go z równowagi. Nauka polega więc na wywoływaniu poszczególnych schematów Układów Regulacji Automatycznej i badaniu ich własności.
Im dalej w las, tym więcej drzew. Zaczynamy od badania członów dynamicznych –> Rozdz. 2…10, a kończymy na  ciekawszych tematach,  takich jak  Regulacja Kaskadowa, Układ Zamknięto-Otwarty, Regulacja Stosunku… Twoja robota to tylko badanie wpływu różnych parametrów na przebiegi czasowe i wyciąganie odpowiednich wniosków.
Będziesz się czuł jak dyspozytor w sterowni Rafinerii Gdańskiej, obserwujący na monitorach proces technologiczny.
Mało tego. Możesz robić rzeczy zakazane. Na przykład wywiercić dziurę w kolumnie przez którą ucieka destylat. Ten przykład jest jednym z podstawowych pojęć automatyki tzw. zakłóceniem. Układ regulacji  skompensuje zakłócenie (uciekający destylat) dodatkowym dopływem. Możesz też tak zmieniać nastawy regulatora PID, żeby powstały drgania niegasnące. W ten sposób bezpiecznie zdobywasz doświadczenie, jak pilot ćwiczący groźne sytuacje na symulatorze Jumbojeta.
Podkreślam. Nie będą to zwykłe “statyczne” rysunki, np. odp. na skok jednostkowy członu inercyjnego, ale prawdziwe kino z plikami mp4! Wszystkie eksperymenty wykonałem w programie SCILAB, ściślej w jego głównej aplikacji Xcos. Po czym zarejestrowałem ich przebiegi przy pomocy programu video Acive Presenter (“kino”). Tak, że nie musisz wchodzić w SCILAB-a, tylko wcisnąć przycisk start video. Gwarantuję Ci, że lepiej poczujesz dynamikę procesu niż na zwykłych wykresach.
UWAGA!!!
Jeżeli do tej pory miałeś mało do czynienia z automatyką, to dalszy tekst tego rozdziału, skrótowo opisujący cały kurs, może trochę onieśmielać. Wtedy nie przejmuj się. Przeczytaj go do końca i przejdź dalej, czyli do Rozdz. 2 Człon Proporcjonalny.

Podstawowe człony dynamiczne → rozdz. 2…10

Każdy z rozdziałów to badanie osobnego członu dynamicznego, od najprostszych do bardziej skomplikowanych. Polega ono na podaniu odpowiedniego sygnału wejściowego x(t) i obserwacji sygnału wyjściowego y(t).

Źródłem sygnału wejściowego x(t) może być:

• generator skoku jednostkowego – najczęściej
• generator sygnału narastającego liniowo
• suwak wirtualnego potencjometru
• impuls Diraca, czyli krótkie stuknięcie wejścia młotkiem

Sygnał wyjściowy y(t) może być obserwowany przez:

• oscyloskop czyli ekran komputera – najczęściej
• cyfrowy miernik wirtualny
• bargraf czyli analogowy miernik wirtualny w postaci czarnej pionowej kreski
  Będziesz kojarzył parametry transmitancji G(s) z odpowiedzią y(t) na sygnał wejściowy x(t). Najczęściej jest nim skok jednostkowy.
  

Przykład animacji.

Rys. 1-1
Człon Oscylacyjny gdy wejściem jest skok jednostkowy
Aby uruchomić animację kliknij trójkącik video.
Z wykresu można odczytać parametr K=2 i T=2sek
Po przeczytaniu rozdziałów 2…10 łatwo przewidzisz np. zachowanie się 2 podobnie wyglądających członów dynamicznych na Rys. 1-2.
Bez matematyki wyższej!

Rys 1-2

Trochę matematyki → rozdz. 11…14

Jeżeli znasz temat to przejdź do rozdziału 15.
Starałem się, żeby kurs był przydatny także dla osób nie znających matematyki wyższej.
Dlatego zawiera on kilka rozdziałów dotyczących pochodnych, całek, prostych równań różniczkowych i rachunku operatorowego. Bo jak tu nie zrozumieć całkowania i różniczkowania, gdy masz do dyspozycji:

• człon różniczkujący który różniczkuje sygnał wejściowy,
• człon całkujący który całkuje sygnał wejściowy.

Rozdz. 11 Różniczkowanie
Jeżeli masz problem z pochodną, to doznasz iluminacji badając człon różniczkujący

Rys.1-3
Sygnałem wejściowym jest parabola x(t)=t².
Jest on dwukrotnie różniczkowany przez układ różniczkujący. Z eksperymentu wynika że pierwszą pochodną x'(t) jest 2t a drugą pochodną x”(t)=2. Zgadza się z teorią.

Rozdz. 12 Całkowanie
Dlaczego akurat skok jednostkowy x(t)=1(t)? Bo trudno o prostszą funkcję i łatwo z niej wyliczyć całkę oznaczoną jako pole S. Potraktujmy całkę oznaczoną jako wyjście y(t) członu całkującego którego wejściem jest x(t)=1(t). Okaże się że y(t)=t(t).
Uwaga:
t(t) to funkcja y(t)=0 dla t<0
                          y(t)=t dla t>0

Rys.1-4
Także całka jako pole pod funkcją stanie się oczywista po zbadaniu członu całkującego.
Pole pod funkcją x(t)=1 to S=1t. A to nic innego jak całka z funkcji x(t)=1(t).

Rozdz. 13 Równania różniczkowe
Wtedy tego jeszcze nie wiedziałeś. Ale z równaniem różniczkowym miałeś już do czynienia   w szkole podstawowej rozwiązując zadanie typu pociąg jedzie z miasta a do miasta b z prędkością v….Przecież prędkość to pochodna drogi a więc…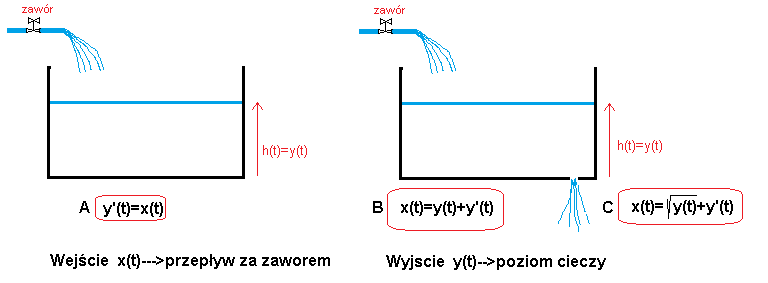

Rys.1-5
Równania różniczkowe poznamy na podstawie mniej trywialnych przykładów:

• A – równanie różniczkowe napełniania zbiornika bez dziury.
• B – równanie różniczkowe uproszczone napełniania zbiornika z dziurą.
• C – równanie różniczkowe dokładne napełniania zbiornika z dziurą.

Pokażę animacje jako rozwiązania powyższych równań różniczkowych.

Rozdz. 14 Rachunek operatorowy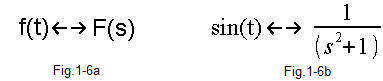

Rys.1-6
Każdej funkcji czasu f(t) można przyporządkować jej transformatę F(s) i odwrotnie–>Rys. 1-6a. Parametr s jest tzw. liczbą zespoloną. Jeżeli nie znasz liczb zespolonych, to traktuj je tymczasowo jak liczby rzeczywiste. Innymi słowy – nie przejmuj się.
Rys. 1-6b jest wersją Rys. 1-6a dla konkretnej funkcji f(t)=sin(t).
Jak się tworzy transformatę F(s) na podstawie f(t)?
Nieważne! Załóżmy, że jest taka mądra książka ze wszystkimi możliwymi parami f(t)<–>F(s).
Rachunek operatorowy ma jedną fajną cechę. Bez niej byłby po prostu bezwartościowy. Jest nią łatwe obliczanie transformaty z pochodnej funkcji f(t), czyli transformaty z f'(t). Wystarczy zwykłe mnożenie F(s) przez s tak jak poniżej:

Rys.1-7
Dzięki temu łatwiej rozwiązuje się równania różniczkowe liniowe*. Są one zamieniane na zwykłe równania algebraiczne, w których występują wielomiany n-tego stopnia zmiennej s. A z nich można już wysnuć wnioski dotyczące układów regulacji automatycznej.
Jakie są przebiegi czasowe, jakie wyjście w stanie ustalonym, jaka stabilność? itd…
*Równania różniczkowe liniowe są przybliżeniem większości układów regulacji. Ich przykładami są równania różniczkowe A i B z Rys.1-5. Nie jest nim natomiast równanie C.

Ogólnie o regulacji → rozdz. 15…22

Rozdz. 15 Więcej o transmitancji i łączenie bloków
Dowiesz się że:

1. Transmitancja G(s) jest odpowiednikiem równania różniczkowego opisującego dany obiekt dynamiczny
2. Z parametrów G(s) łatwo wyznaczymy wzmocnienie K w stanie ustalonym
3. Transmitancje bloków połączonych:
   – szeregowo
   – równolegle
   – z ujemnym sprzężeniem zwrotny,
   można zastąpić pojedynczą transmitancją zastępczą Gz(s).

Rozdz. 16 Jak działa sprzężenie zwrotne?
Czytasz sobie instrukcję pralki, komórki czy czegoś tam jeszcze i masz problemy. Chociaż gość pisze mądrze i językiem pięknym, ale czegoś brakuje. No właśnie. Osoba pisząca instrukcje siedzi głęboko w temacie, bo tylko tym się zajmuje. Dla niego działanie urządzenia jest oczywiste jak działanie cepa. Nie chce po prostu obrażać Użytkownika dokładnym tłumaczeniem jak to działa.
Podobnie jest z ujemnym sprzężeniem zwrotnym. Przecież to wszystko wynika z pokazanego niżej wzoru Rys. 1-8c! Dotyczy on transmitancji Gz(s) układu z ujemnym sprzężeniem zwrotnym. W dodatku bardzo łatwo się ten wzór wyprowadza.
Ale jak na prawdę  działa ujemne sprzężenie zwrotne? Ten sam sygnał y(t) na wyjściu i  wejściu? Wąż jedzący własny ogon? Dlaczego sygnał wyjściowy y(t) stara się naśladować sygnał wejściowy, tzw. wartość zadaną x(t)?
Dobre zrozumienie tego problemu to zrozumienie istoty automatyki. Bez tego różne Nyquisty, Hurwitze, przestrzenie stanów… są nic nie warte.
Przejdźmy więc do zasady działania cepa.

Rys.1-8
Rozdział rozpoczyna się dodatnim sprzężeniem zwrotnym z Rys.1-8a, które łatwo poddaje się intuicji. Dowiesz się, że nie zawsze układ z dodatnim sprzężeniem zwrotnym jest niestabilny. Staje się nim dopiero przy większych wzmocnieniach K*.
Będziesz wiedział dlaczego w układzie z ujemnym sprzężeniem zwrotnym na Rys.1-8b, wyjście y(t) “stara” się naśladować wejście x(t). Najważniejsze to zrozumienie zasady, że układ dąży do stanu ustalonego, w którym:
y(t)=K*e(t)
Tylko wtedy to równanie jest spełnione. Gdyby y(t) z jakichś powodów wzrosło, to e(t)=x(t)-y(t)  zmalałoby, czyli y(t)=K*e(t) też by zmalało. W ten sposób powstanie równowaga y(t)=K*e(t).
Podobnie jak wahadło, które dąży do stanu najniższego położenia. Przekonasz się, że wartości K*e(t) oraz y(t) “lgną do siebie”. Na początku skoku x(t) różnica między K*e(t) a y(t) jest duża, potem się zmniejsza aż do stanu równowagi w którym y(t)=K*e(t)!
Jeżeli “lgnące do siebie” przebiegi K*e(t) oraz y(t) będą dla Ciebie oczywiste, to znaczy że czujesz ujemne sprzężenie zwrotne! Ze stanu równowagi y(t)=K*e(t) wynika wzór na wzmocnienie Kz układu zamkniętego w stanie ustalonym Rys.1-8d. Jest on zresztą szczególnym przypadkiem transmitancji Gz(s) układu zamkniętego z Rys.1-8c.
Nie zawsze przebieg y(t) kończy się stanem równowagi, lecz drganiami niegasnącymi. Układ jest niestabilny. Wtedy wzór na Kz jest trochę bez sensu, ale nie do końca. Mianowicie oscylacje mają składową stałą c=Kz*x(t) gdzie x(t) jest skokiem jednostkowym.
*K jest wzmocnieniem obiektu G(s) w stanie ustalonym.

Rozdz. 17. Niestabilność, czyli jak powstają drgania
Dojdziemy do wniosku, że przyczyną niestabilności jest opóźnienie między sygnałem wejściowym a wyjściowym.
Najłatwiej przekonasz się o tym sterując czystym opóźnieniem.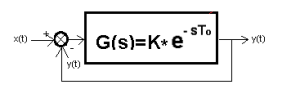

Rys.1-9
Okaże się, że gdy wzmocnienie jest:

• K<1 to układ jest stabilny
• K=1 to układ jest na granicy stabilności
• K>1 to układ jest niestabilny
  

Rys. 1-10
Przykład układu niestabilnego gdy K>1
Krótki impuls x(t) wytrąca układ z równowagi
Czy nie przypomina to kryterium Nyquista, o którym będzie mowa w następnym rozdziale?
Najczęściej mamy do czynienia z obiektami wieloinercyjnymi w których opóźnienie jest “rozmyte”.
Zasada nie jest już taka prosta, ale podobna.
Jeżeli na Rys. 1-9 zamiast “czystego” opóźnienia będzie np. człon trójinercyjny to stwierdzimy, że gdy:

• K jest małe, to układ jest stabilny
• K jest średnie, to układ jest na granicy stabilności
• K jest duże, to układ jest niestabilny
  

Wniosek: Duże wzmocnienie i bezwładność obiektu sprzyjają niestabilności.

Rozdz. 18. Charakterystyka amplitudowo-fazowa
W sposób najbardziej naturalny poznasz pojęcie charakterystyki amplitudowo – fazowej.  Wyznaczona w ten sposób amplituda i faza układu otwartego dla całego zakresu częstotliwości zawiera w sobie łatwą do odczytania informację o stabilności układu zamkniętego.

Rozdz. 19. Kryterium stabilności Nyquista
Układ otwarty jest z reguły stabilny. Może stać się niestabilnym dopiero po zamknięciu go pętlą sprzężenia zwrotnego. Kryterium Nyquista potrafi przewidzieć na podstawie charakterystyki amplitudowo-fazowej układu otwartego (który jest “łatwiejszy” niż zamknięty) stabilność układu zamkniętego.
Przy okazji w sposób najbardziej naturalny poznasz pojęcie charakterystyki amplitudowo-fazowej. Wyznaczysz ją doświadczalnie dla konkretnego członu inercyjnego, podając na jego wejście sinusoidy o różnych częstotliwościach. Dlatego Nyquist należy kryteriów częstotliwościowych.

Rozdz. 20. Kryterium stabilności Hurwitza
W odróżnieniu od Nyquista, kryterium Hurwitza należy do algebraicznych. Badamy stabilność transmitancji G(s) na podstawie współczynników jej mianownika-wielomianu M(s). Kryterium Hurwitza nie jest trudne, ale dość męczące. Od biedy możesz więc ominąć ten temat i jechać dalej. Najważniejsze w tym kursie to cała reszta–>rozdziały 21…31.

Rozdz. 21. Regulacja dwupołożeniowa
Algorytm sterowania jest bardzo prosty
Gdy sygnał wyjściowy y(t) jest:
– większy od wartości zadanej x(t)—>zmniejsz sygnał sterujący s(t)
– mniejszy od wartości zadanej x(t)—>zwiększ sygnał sterujący s(t)
Będziesz się męczył pełniąc funkcję Pana Regulatora Dwupołożeniowego. A i tak przekonasz się, że głupi przekaźnik z elementem porównującym robi to znacznie lepiej. Wadą regulacji dwupołożeniowej jest ciągłe przełączenia się regulatora na wartość MAX albo MIN w stanie ustalonym.

Rys. 1-11
Przykład regulacji dwupołożeniowej z zakłóceniem z(t)=+30°.
Do 15 sekundy układ stara się utrzymać temperaturę wokół zwartości zadanej x(t)=+50°C. W 15 sekundzie pojawiło się zakłócenie tj. dodatkowe grzanie z(t)=+30°C. Jak widzisz zakłócenie zostało stłumione. Tzn. w dalszym ciągu utrzymywana jest średnia temperatura y(t)=+50°C. Okresy grzania gdy s(t)=100°C są krótsze niż chłodzenia s(t)=0°C.
Uwaga
Powyższe sterowanie trochę różni się od algorytmu podanego na wstępie. Tu uwzględnia tzw. histerezę związaną z żółtymi liniami na Rys. 1-11.

Rozdz. 22. Regulacja ciągła
Ten typ regulacji zapewnia już stały sygnał sterujący z regulatora i stały sygnał wyjściowy w stanie ustalonym. Też się pomęczysz jako Pan Regulator Ciągły i też nabierzesz kompleksów względem głupiego wzmacniacza różnicowego, pełniącego funkcję regulatora.
Regulator Ciągły będzie dążył do stanu równowagi:
y(t)=Kz*x(t)
w którym x(t) jest skokiem jednostkowym a Kz jest wzmocnieniem z Rys.1-8d.

Créme de la créme, czyli regulacja ciągła PID–>rozdz. 23…27

Generalnie to bazuję na intuicji pisząc np. “regulator myśli, że coś tam i reaguje tak a nie tak”. Próbuję bardzo dokładnie wytłumaczyć działanie regulatora. a zwłaszcza za co odpowiadają nastawy Kp,Ti oraz Td. Na pewno pomoże tu ręczne strojenie regulatorów. Będziesz szukał optymalnej* odpowiedzi na skok sygnału wejściowego, albo na zakłócenie. Spójnik albo pojawił się nieprzypadkowo.
Nie przeraź się wielkością rozdziałów 23…27, ale wszystkie doświadczenia są powtarzalne z różnymi parametrami.
Będziemy szukać optymalnych nastaw dla obiektu:

• jednoinercyjnego,
  
• dwuinercyjnego,
  
• trójinercyjnego.

Zbadamy także wpływ zakłóceń z(t) które będą naprawdę potężne, raczej niespotykane w prawdziwych układach. Będzie to z(t)=+0.4 (grzanie) i z(t)=-0.4(chłodzenie)
*Są różne kryteria optymalności. Nam zależy na tym, żeby układ doszedł w miarę szybko do stanu ustalonego, nawet kosztem niewielkich oscylacji.

Rozdz. 23 Regulacja P
Przekonasz się, że ta regulacja nie jest dokładna, zawsze powstaje uchyb regulacji e. Można go zmniejszyć zwiększając jedyną nastawę tego regulatora – wzmocnienie Kp. Mogą wtedy pojawić oscylacje, a nawet niestabilność. W stanie równowagi będzie osiągnięty sygnał wyjściowy y(t) z taką wartością: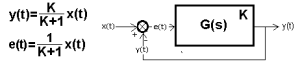

Rys.1-12
Tu K=Ko*Kp jest wzmocnieniem statycznym całej pętli otwartej, czyli uwzględniającej wzmocnienie w stanie ustalonym obiektu Ko i wzmocnienie Kp regulatora. Wzory pokazują stan ustalony dla skoku x(t). Dla dużego K zbliżają się do bardzo pożądanych w automatyce wzorów:
y(t)=x(t)
e(t)=0
Wtedy sygnał wyjściowy y(t) naśladuje w stanie ustalonym sygnał wejściowy x(t) lub, co na jedno wychodzi, mamy zerowy uchyb e(t).

Rozdz. 24 Regulacja PD
Daje taki sam uchyb regulacji jak Regulacja P, za to składowa różniczkująca D rewelacyjnie poprawia własności dynamiczne. Zmniejsza oscylacje i z powodzeniem walczy z niestabilnością. Za chwilę się przekonasz.

Rys.1-14
Przykład regulacji PD z zakłóceniem dodatnim z(t)=+0.5.
A nie mówiłem? Porównaj z regulacją P z Rys. 1-12. Uchyb statyczny niezerowy jak dla regulacji P. Za to rewelacyjnie poprawia przebieg regulacji. Tu zwłaszcza na skok jednostkowy x(t). Trochę gorzej tłumi zakłócenie z(t)=+0,5. Układ szybko reaguje na x(t), ale wolniej na z(t).   Ale zawsze można tak dobrać Kp i Td, żeby było odwrotnie. Tzn. Szybko reaguje na z(t) ale wolniej na x(t).

Rozdz. 25 Regulacja I
Jej algorytm działania jest łatwiejszy niż Regulacji P i podobny do regulacji dwupołożeniowej:

• x(t)>y(t)–>stopniowo zwiększaj sygnał sterujący
  
• x(t)<y(t)–>stopniowo zmniejszaj sygnał sterujący 

Prędkość zmniejszania/zwiększania jest proporcjonalna do uchybu e(t)=x(t)-y(t). Gdy e(t)=0 to prędkość jest zerowa, czyli jest stan ustalony. W przeciwieństwie do regulacji dwupołożeniowej, sygnał sterujący w stanie ustalonym jest stały. Najważniejszą cechą jest zerowy uchyb regulacji w stanie ustalonym. Często początkujący automatycy mają z tym  problem. Na wejściu jest zero, a na wyjściu “nie zero”?  Regulacja I jest bardzo wolna i raczej nie stosowana w praktyce.

Rys.1-15
Przykład regulacji I. Rzeczywiście sprowadza uchyb do 0. Ale jaki wołowaty! Porównaj z PD z Rys. 1-13

Rozdz. 26 Regulacja PI
Regulacja P jest szybka ale nie sprowadza uchybu do 0, za to I sprowadza do uchyb do 0, ale jest wolna. To stwórzmy kombinację P oraz I zwaną PI która będzie szybka (ale nie tak jak P) za to sprowadza uchyb e(t) do do 0. Rozpoczniemy od dydaktycznego PI który zmajstrowałem. Zaczyna jako P i w pewnym momencie zmienia się na I. Potem okaże się, że prawdziwe PI działa podobnie, tylko przemiana z P na I, występuje w sposób ciągły.

Rys.1-16
Przykład regulacji PI z zakłóceniem dodatnim z(t)=+0.5
Uchyb zerowy i w miarę szybko dochodzi do stanu ustalonego.

Rozdz. 27 Regulacja PID
Po dodaniu do regulatora PI składowej różniczkującej D otrzymamy regulację PID która:

• też sprowadza uchyb do 0:
• robi to jednak znacznie szybciej niż PI, a tym bardziej P i jeszcze “tym bardziej” I 

Składowa D zapobiega niestabilnościom i przeregulowaniom.
Przy skoku jednostkowym każdy regulator PID

• zaczyna ja regulator PD,
• potem składowe P i D stopniowo zanikają do 0 a składowa I rośnie od 0 do stanu ustalonego y(t)=x(t),
• w stanie ustalonym  kończy zawsze jako regulator I.

Rys.1-17
Przykład regulacji PID z zakłóceniem dodatnim z(t)=+0.5
Uchyb jest zerowy i najszybszy  ze wszystkich. Tu zakłócenie jest już całkiem nieźle tłumione.

Rozdz. 28 Dobór nastaw regulatorów
Pierwszą metodę tj. ręczną, poznałeś w rozdziałach 23…27. Była zastosowana głównie po to, żebyś czuł, czym jest ten dobór, żebyś wiedział co robią nastawy Kp, Ti, Td. Są ludzie którzy montują szafy, regulatory, zawory i to wszystko łączą kablami w całość zgodnie z projektem automatyki.
Są też i tacy którzy uruchamiają te układy, usuwają błędy montażu i oprogramowania. Powodują, że Układ Regulacji ożywa.
Nie chcę twierdzić, że jest to elita automatyki. Może to niepoprawne, ale niektórzy tak myślą. I właśnie Ci ludzie stroją regulatory, tak żeby system reagował jak najszybciej i to w miarę dokładnie. Potem układ pracuje latami. Może to robić dokładnie i szybko, lub niedokładnie i wolno. I dziwią się ludziska, że produkt jednej firmy jest dobry i drogi a drugiej dziadowski i tani. Dlatego tak odpowiedzialna jest praca stroicieli fortepianów, pardon regulatorów PID.
Przedstawię trochę staromodne metody wymyślone jeszcze w czasie II wojny światowej przez niejakiego Zieglera i Nicholsa:

• Metoda odpowiedzi skokowej.
• Metoda cyklu granicznego.

Każda jest przykładem innej szkoły. Pierwsza wymaga opisu matematycznego, czytaj transmitancji Go(s) obiektu. Druga tylko zbadania obiektu, a ściślej zmierzenia okresu drgań przy pewnym wzmocnieniu krytycznym. Jest więc mniej wybredna co do dokładnej znajomości obiektu.
Żeby zakończyć temat, to wiele współczesnych regulatorów (większość?) ma wbudowany mechanizm samostrojenia. Obserwując wejście i wyjście, regulator sam zmienia parametry Kp, Ti, Td, tak żeby było dobrze. Są one tak mądre, że bez kija lepiej nie podchodź. Zaufajmy tylko, że liczne prace doktorskie i habilitacyjne zapisane w oprogramowaniu regulatorów PID wiedzą jak sterować, żeby było dobrze.

Jeszcze to musisz wiedzieć → 29…31

Pozostało jeszcze kilka ważnych tematów, które są potrzebne do zrozumienia istoty automatyki.

Rozdz. 29 Analiza Zakłóceń
Głównym sygnałem działającym na Układ Regulacji jest wartość zadana x(t). Ale są też inne tzw. zakłócające z(t), które cały czas kombinują, jakby tu zaszkodzić. Ściślej, Żeby np. temperatura wyjściowa y(t) zamiast zadanej przez x(t)=+100°C była np.  y(t)=+96°C. W stanie ustalonym oczywiście!
Interesuje nas tylko zakłócenie działające na obiekt Go(s). Bo jeżeli zakłócenie z(t) działa na regulator i dodaje się do wartości zadanej x(t), to strach nawet pomyśleć! Tak jakby szpieg wkradł się do sztabu wrażej armii i zaczął wydawać rozkazy. Na szczęście łatwiejsze jest zabezpieczenie sztabu niż całej armii, tak jak łatwiej zabezpiecza się przed zakłóceniem malutki regulator PID niż duży obiekt Go(s).
Wróćmy jeszcze do obiektu Go(s). Okaże się, że przesuwające się w prawo zakłócenie z(t) daje coraz bardziej wyraźny wpływ na y(t).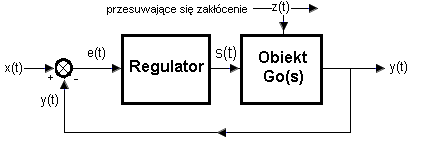

Rys.1-18

Rozdz. 30 Struktury układów regulacji
Jakość regulacji możemy poprawić nie tylko tylko strojąc PID-a, ale także zmieniając strukturę układu regulacji.
Typowe Struktury to Układ:

1. Otwarty
2. Otwarty z Kompensacją
3. Zamknięty
4. Zamknięty z Kompensacją
5. Kaskadowy
6. Regulacji Stosunku

Cały dotychczasowy kurs dotyczył układu Otwartego i Zamkniętego. Dlatego w skrócie omówimy pozostałe.
2. Otwarty z kompensacją: Sterujesz piecem elektrycznym w którym jest łatwe do zmierzenia główne zakłócenie-wahania sieci. Należy więc to zakłócenie zmierzyć np. +37V amplitudy i skompensować napięciem -37V amplitudy. Sam piec “myśli” że nic się nie stało i nawet nie będzie widać wpływu zakłócenia. Zauważ, że nie ma tu sprzężenia zwrotnego, stąd inna nazwa “sprzężenie do przodu” ( “feed forward“) w przeciwieństwie do poczciwego “sprzężenia zwrotnego” (“feedback”)
4. Zamknięty z kompensacją: Układ Otwarty z kompensacją nie tłumi pozostałych zakłóceń (które nie są mierzone). Należy więc całość zamknąć zwykłą pętlą sprzężenia zwrotnego. I tak główne zakłócenie-wahania sieci będzie bardzo szybko tłumione przez kompensację, a pozostałe będą wolno tłumione przez zwykłe sprzężenie zwrotne.
Inna nazwa układu regulacji to Zamknięto-Otwarty.
5. Kaskadowy: Ta regulacja jest możliwa, gdy da się wyodrębnić pewną część obiektu, na którą działa zakłócenie lub zakłócenia. I w tym podobne jest do poprzedniego- Zamknięty z kompensacją. Nie jest natomiast  konieczny pomiar zakłócenia.  Tę część można więc zamknąć wewnętrzną pętlą sprzężenia zwrotnego z osobnym regulatorem podrzędnym. Często wystarczy tu zwykły regulator P. Całość zamykamy zewnętrzną pętlą z regulatorem nadrzędnym– najczęściej typu PID. Zauważ, że  regulator P szybko stłumi zakłócenie w pętli wewnętrznej, zanim informacja o nim dojdzie przez duże bezwładności pozostałej części obiektu do regulatora PID. Regulator PID tłumi wszystkie pozostałe zakłócenia, także ew. niedoskonałości tłumienia regulatora P.
Zasada jest więc podobna do działania firmy w której prezes-regulator nadrzędny tłumi wszystkie zakłócenia a kierownik-regulator podrzędny tłumi tylko “prywatne” zakłócenia jego działu. Dobry kierownik tak szybko je stłumi, że często nie dojdzie to do prezesa. I słusznie, bo Prezes jest od spraw wielkich.
6. Regulacji Stosunku: Przykład. Kolor danej farby zależy od stosunku  2 ich podstawowych składowych. Należy więc napełnić zbiornik mieszalni 2 przepływami różnych farb, których stosunek przepływów jest stały niezależnie od zakłóceń.

Rozdz. 31 Wpływ nieliniowości na regulację
Do tej pory badaliśmy układy liniowe. W nich regulator PID w celu szybkiego działania może dać tak duży sygnał, jaki jest mu potrzebny. W kursie wielokrotnie spotkasz się z sytuacją, w której piec potrzebuje np. 1 kW żeby osiągnąć temperaturę y(t)=+100°C w stanie ustalonym. Ale w stanach przejściowych PID daje krótkie szpile nawet po 1000 kW, po to by szybko dojść do tych +100°C.
Prawdziwe systemy mają ograniczenia. Piec może dać max tylko 3 kW, więcej byłoby nieuzasadnione ekonomicznie. Wiadomo, że odpowiedź y(t) w tym konkretnym przypadku 3 kW, już nie będzie taka cacy.  Ale czy będzie dużo gorsza?
Odpowiedź na to pytanie jest właśnie celem tego tego rozdziału. Ma też wykazać, że główną nieliniowością wpływającą negatywnie na jakość regulacji, są ograniczenia Wzmacniacza Mocy za regulatorem. Wzmacniacz ten ma też inną nazwę – Człon Wykonawczy