Preliminary Automatics Course
Chapter 9. Differential Unit
Chapter 9.1 Introduction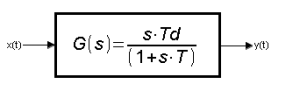
FIg. 9-1
Differential Unit transfer function G(s). More strictly – Ideal Differential Unit transfer function G(s).
Differential Unit reacts for input signal x(t) changes–>x(t) speed. It doesn’t react for absolute x(t) value! Differential Unit is an ideal beginners teaching aid for differential calculus.
The output Differential Unit signal y(t) is proportional to the x(t) speed. To the x(t) derivative x'(t) in other words.
Chapter 9.2 Input x(t)signal-ramp type
Call Desktop/PID/01_podstawowe_człony_dynamiczne/04_człon_różniczkujący/01-różniczkujący_oscyloskop_1narastanie.zcos
FIg. 9-2
What’s the Dummy Clls block. Don’t ask please. It must be and the subject is over.
You can’t build the ideal Differential Unit (FIg. 9-1) by the general transfer function G(s) (for example Fig. 7-1 chapter 7) modification. You have to use the special ideal differentiating Scilab block. You set the Td parameter (differentiation intensity) by the proportional unit modification.
Click „Start”
FIg. 9-3
Wow! First impression. It’s such an integrating unit (Fig. 8-7) but see these both figures more thoroughly. The black input x(t) is a ramp type and red output y(t) is a step type here. The Fig. 8-7 shows that differentiation is conversely to integration and vice versa.
Important for differentiating unit G(s)=s
The output signal y(t) is a speed of the input signal x(t)
The speed of the black x(t) on the FIg. 9-3 is x'(t)=1/sec –>red y(t)=1
Td parameter definition
The time when x(t) is a ramp type and x(t)=y(t)
Td=1sec in the FIg. 9-3 because x(t)=y(t) after Td=4-3=1sec.
Please note that Td doesn’t depend on x(t) slope (speed). When speed is doubled–>the y(t) is doubled too and Td doesn’t change.
Repeate please this experiment with the doubled x(t) speed
Set the rightmouse the ramp slope=2
FIg. 9-4
Click „Start”
FIg. 9-5
The x(t) speed is doubled so the y(t)=2 is doubled too.
Chapter 9.3 Signal x(t) „grows, stands and fells”
Call Desktop/PID/01_podstawowe_człony_dynamiczne/04_człon_różniczkujący/02-różniczkujący_oscyloskop_narast_staly_opad.zcos
FIg. 9-6
Click „Start”
FIg. 9-7
0…2 sec x(t)=0 is steady–>y(t)=0 because x'(t)=0
2…4 sec x(t) grows with the speed =1/sek–>y(t)=+1 because x'(t)=+1
4…6 sek x(t)=1 is steady –>y(t)=0 because x'(t)=0
6…10 sek x(t) fells with the (negative) speed =-1/sek–>y(t)=-1 because x'(t)=-1
The experiment is ideal to understand the derivative concept.
Chapter 9.4 Signal x(t) with 2 speeds
Call Pulpit/PID/01_podstawowe_człony_dynamiczne/04_człon_różniczkujący/03-różniczkujący_oscyloskop_2narastania.zcos
FIg. 9-8
Wciśnij „Start”
FIg. 9-9
The x(t) speed doubled–> the y(t) doubled
Chapter 9.5 Signal x(t) with 4 speeds
Call Desktop/PID/01_podstawowe_człony_dynamiczne/04_człon_różniczkujący/04-różniczkujący_oscyloskop_4narastania.zcos
FIg. 9-10
Wciśnij „Start”
Rys. 9-11
The x(t) speed fourfolded–> the y(t) fourfolded.
The x(t) is similar to parabola–> the y(t) is similar to linear function.
And when the x(t) is a parabola? Do you foresee the y(t)?
Chapter 9.6 Signal x(t) is a parabola
Call Desktop/PID/01_podstawowe_człony_dynamiczne/04_człon_różniczkujący/05-różniczkujący_oscyloskop_kwadrat.zcos
Rys. 9-12
The x(t) is a parabola type function.
Click „Start”
Fig. 9-13
The differentiating unit confirms the formula for the derivative of the parabola function.
Chapter 9.7 x(t)=sin(t)
Cal Desktop/PID/01_podstawowe_człony_dynamiczne/04_człon_różniczkujący/06-różniczkujący_oscyloskop_sinusoida.zcos
Fig. 9-14
Click „Start”
Fig. 9-15
x(t)=sin(t) y(t)=x'(t)= sin'(t)=cos(t)
Treat y(t) as a speed of the x(t).
For example;
sin(0)=0 and the speed is max–>sin'(0)=max=cos(Π/2)=1
sin(Π/2)=1 = max and the speed is 0–>sin'(Π/2)=cos(Π/2)=0
…
etc…
Chapter 9.8 x(t) is a sigle rectangular pulse
Call Desktop/PID/01_podstawowe_człony_dynamiczne/04_człon_różniczkujący/07-rozniczkujacy_oscyloskop_1_impuls.zcos
Fig. 9-16
Click „Start”
Fig. 9-17
The x(t) speed in the t=3 sec = +infinity–>the y(t)=+infinity
The x(t) speed in the t=6 sec= -infinity–>the y(t)=-infinity
The x(t)=0 other t–> y(t)=0
Chapter 9.9 Summary
The differentiating unit reacts for the input x(t) speed (derivative) i.e. for the x'(t)
Fig. 9-18
Electrical example-solenoid