8. Fourier series of an even square wave. - How does it work?/Jak to dziala?

Rotating Fourier Series

Chapter 8. Fourier series of an even square wave

Chapter 8.1 Introduction
So far, we have studied the function f(t), in which all harmonics were visible in the formula, e.g. f(t)=1.3+0.7cos(2t)+05.cos(4t).
What if harmonics are not visible in the function f(t)?
As, for example, in a square wave f(t) with amplitude A=1, pulsation ω=1/sec, initial phase ϕ=0 and duty cycle w=50%.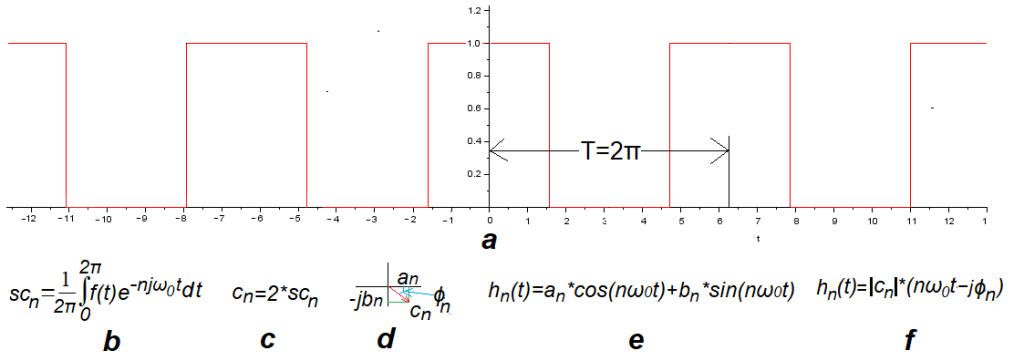

Fig.8-1
Even square wave and harmonic formulas
Fig.8-1a
Even square wave f(t) A=1, ω=1/sec, ϕ=0 and w=50%.
A few words of explanation. The parameters A, ω and ϕ are typical for trigonometric functions. It is difficult to assign them, for example, to a quadratic function. But a square wave does! The parameters A=1 and ω=1/sec are obvious. I will only add that ω=1/sec corresponds to the period T=2πsec. And ϕ=0 means that the wave starts in the “upper half of the rectangle“, just like ϕ=0 in the “upper half of the cosine wave”.
Harmonic formulas
In the next points we will analyze the trajectories F(n*jω0t) and time charts of the square wave for n=0…8. Similarly to what we did before with trigonometric functions. But first, a few words on how to read the nth harmonic hn(t) from the centroid of the nth trajectory F(njω0t).
Fig.8-1b
Formula for the nth centroid scn of the trajectory F(n*jω0t)
In this chapter, the centroids of scn agree with intuition and we will only assume that they are true. In Chapter 11, we will calculate them precisely with the WolframAlfa program.
Fig.8-1c
Formula for the nth complex coefficient of a Fourier series cn
This is after doubling the centroid scn! Treat this as the complex amplitude for the nth harmonic.
Note
The formula is true for n=1,2,3…
For n=0
c0=sc0=a0 and this is the average of f(t) over the period.

Chapter 8.2 Even square wave f(t) and its trajectory F(njω0t) for n=0, i.e. F(0j1t)

Fig.8-2
The trajectory F(0j1) of the function f(t) of an even square wave, i.e. with the parameters:
A=1-amplltude
ω0=1/sec-pulsation corresponding to the period T=2πsec≈6.28sec.
ϕ=0
50%-filling
Fig.8-2a
The trajectory F(0j1t) corresponds to the trajectory F(njω0t) for n=0 and ω0=1/sec.
A stationary Z plane, where on the real axis Re Z the vector changes according to. the function f(t) shown
in Fig.8-2b. In other words, these are jumping movements “back and forth” on the real axis Re Z between the points (0,0) and (1,0).
Fig.8-2b
Time chart f(t) of an even square wave.
Notice that the waveform begins halfway through the half-cycle. Just like the cosine function. Both animations in Fig. a and b describe the same thing. Read the parameters A,ω0,ϕ and filling parameter. Animating b is easier, but animation a is also possible. From the time chart it is possible to calculate, even without integrals, the coefficient c0=a0=0.5 of the Fourier Series as the average value of f(t) for 0…2π. See Fig.8-1c.
In the next subchapters, the Z plane will start rotating at speeds ω=-nω0, i.e. -1/sec,-2/sec…-8/sec in the “clockwise” direction. The end of the vector will draw trajectories F(njω0). From them we will read the harmonics for the nω0 pulsation. As in previous chapters, only instead of f(t)=combination of sines and cosines, it will now be f(t)=square wave

Chapter 8.3 First harmonic of an even square wave h1(t) =a1*cos(1t).
Section 8.3.1 Trajectory of F(njω0t) of an even square wave for n=1 and ω0=1/sec, i.e. F(1j1t).

Fig.8-3
Trajectory F(1j1t) of an even square wave
Fig.8-3a
The radius R=1 as a vector (1,0) rotates with speed ω=-1/sec around the point (0,0) in time T=2π sec. The entire complex plane Z rotates with it. But be careful! The axes of the Re Z and Im Z planes don’t rotate! The end of the vector would draw an entire circle unlike the semi-circle in Fig.8-3c. The average value of the sum of rotating vectors during 1 revolution, i.e. during 2π sec, is the zero vector z=(0,0). The z parameter is the so-called centroid of the trajectory, i.e. circle. Here z coincides with the centroid scn known from physics.
Fig.8-3b
Trajectory F(1j1t)=f(t)*exp(-1j1t) as a rotating vector modulated by the function f(t).
The function f(t) is the square wave of Fig.8-2b. Look at Fig.8-2a and imagine that the Z plane starts rotating at a speed of ω=-1/sec. As a reminder, the Re Z and Im Z axes are stationary! This will create a rotating vector F(1j1t)=f(t)*exp(-1j1t). The Z plane will make 1 revolution, and the radius R=1 will make 2 “quarter turns” with a break of 1π sec in between. This is equivalent to one “half-turn”.
Fig.8-3c
The trajectory of F(1j1t) as a semicircle drawn by the end of the vector in Fig. 8-3b.
Now imagine that during 1 rotation of the Z plane, i.e. by an angle of 0…2π, all vectors are summed (vectorically!) and their average is calculated. Some sc1 vector will be created. Will it be sc1=(0,0) as in Fig.8-3a? Probably not, but it will definitely lie somewhere on the Re Z axis between (0,0) and (1,0). Rather closer to (0,0) than (1,0). It will be the vector sc1=(1/π, 0)! Otherwise, the centroid sc1=(1/π, 0) of the trajectory F(1j1t). We will precisely calculate the sc1 parameter of the trajectory using the WolframAlfa program in Chapter 11.
Note to Fig. 8-3b,c
The above animations suggest that the upper and lower “quadrants” of the trajectories are separated by a gap T=πsec. But this is only the case at the beginning at time t=0…2π sec! Later, there is no break and the movement along the trajectory is continuous.
Chapter 8.3.2 First harmonic against the background of an even square wave, i.e. c0+h1(t) or in other words, the first approximation of an even square wave.
Acc. to Fig. 8-1c the constant component c0 is the average over the period T=2π that is, c0=a0=0.5 . You can calculate it even without integral calculus.
c1 is the complex amplitude of the first harmonic
c1=2*sc1=(2/π,0) i.e. a1=2/π and b1=0
Acc. to Fig. 8-1e
h1(t)=(2/π)*cos(1t)≈0.637cos(1t)

Fig.8-4
S1(t)=c0+h1(t) i.e. the first harmonic with a constant component c0=0.5 against the background of a square wave. This is also a first approximation to our even 50% square wave.

Chapter 8.4 Second harmonic of an even square wave, or rather its absence because
c2=0 –>h2(t)=a2*cos(2t)=0.
Chapter 8.4.1 Trajectory F(njω0t) of an even square wave for n=2 and ω0=1/sec, i.e. F(2j1t).
The Z plane rotates at a speed of ω=-2/sec

Fig.8-5
Trajectory F(2j1t) of an even square wave
Fig.8-5a
The radius R=1 as a vector (1,0) rotates with a speed ω=-2/sec around the point (0,0) and will complete 2 revolutions in time T=2π sec.
Fig.8-5b
Trajectory F(2j1t)=f(t)*exp(-2j1t) as a rotating vector modulated by the function f(t). In 2π sec, the Z plane will make 2 revolutions, but the radius R=1 will only make 2 “half-turns” with a break of 1π sec in between.
Fig.8-5c
The trajectory of F(2j1t) as a circle drawn by the end of the vector in Fig. 8-5b.
Obviously sc2=0. Note that from the circle itself the value sc2=0 is not obvious! After all, the circle could have been drawn, for example, 1.5 times. Fortunately, this 1 complete revolution, although with a break in the middle, is visible in Fig. 8-5b
Note
sc2=0 and therefore the harmonic for ω=2/sec does not exist.

Chapter 8.5 Third harmonic of an even symmetric square wave h3(t) =a3*cos(3t).
Chapter 8.5.1 Trajectory F(njω0t) of an even square wave for n=3 and ω0=1/sec, i.e. F(3j1t).
The Z plane rotates at a speed of ω=-3/sec

Fig.8-6
Trajectory F(3j1t) of an even square wave
Fig.8-6a
The radius R=1 as a vector (1,0) rotates with a speed ω=-3/sec around the point (0,0) and will complete 3 revolutions in time T=2π sec.
Fig.8-6b
Trajectory F(3j1t)=f(t)*exp(-3j1t) as a rotating vector modulated by the function f(t).
In time T=2π sec, the Z plane will make 3 revolutions, but the radius R=1 will only make 2 times “3/4 revolutions” with a break of 1π sec in between. It will turn out that during T=2π sec, the radius R=1 stays longer in the left half-plane than in the right one. Therefore, its average value as a vector will be (-1/3π, 0)
Fig.8-6c
The trajectory of F(3j1t) as a circle drawn by the end of the vector in Fig. 8-6b.
The centroid sc3=(-1/3π, 0) results from the summation of the vectors in Fig. 8-6b and their average at time T=2π sec when 3 revolutions of the Z plane are made. Its value is negative, unlike in Fig.8-3b, where the vector has made 2 “quarter turns” only on the positive Z half-plane.
Note
In the next subchapters there will be no such detailed description of the trajectory F(njω0t).
The reader will notice that:
for even rotational speeds of the Z plane, i.e. for ω=-4/sec, -6/sec, -8/sec…
scn parameters are zero, i.e. there are no harmonics for even ω.
for odd rotational speeds of the Z plane, i.e. for ω=-5/sec, -7/sec…
scn parameters are non-zero and decrease to zero when ω=-∞. In other words, the harmonic amplitudes decrease to zero as the frequency increases to infinity.
Chapter 8.5.2 Third harmonic against the background of an even square wave, i.e. c0+h3(t).
Acc. to Fig. 8-1c
c3 is the complex amplitude of the third harmonic
c3=2*sc3=(-2/3π,0) i.e. a3=-2/3π and b3=0
Acc. to Fig. 8-1e
h3(t)=-(2/3π)*cos(3t)≈-0.212cos(3t)

Fig.8-7
c0+h3(t)=0.5-(2/3π)*cos(3t)+0.5
That is, the third harmonic with a constant component c0 against the background of a square wave.
Chapter 8.5.3 Third approximation of an even square wave, i.e. S3(t)=c0+h1(t)+h3(t).

Fig.8-8
S3(t)=c0+h1(t)+h3(t)
The third approximation is more similar to a square wave than the first one in Fig.8-4
What about the second one? So from S2(t)=c0+h1(t)+h2(t)? It is the same as the first one, i.e. S1(t)=c0+h1(t) because h2(t)=0 and we ignore it. It is similar with the fourth, sixth approximation…, because h4(t)=h6(t)=…=0.

Chapter 8.6 Fourth harmonic of an even symmetric square wave, or rather its lack because
c4=0 –>h4(t)=a4*cos(4t)=0.
Chapter 8.6.1 Trajectory F(njω0t) of an even square wave for n=4 and ω0=1/sec, i.e. F(4j1t).
The Z plane rotates at a speed of ω=-4/sec

Fig.8-9
Trajectory F(4j1t) of an even square wave
Fig.8-9a
The radius R=1 as a vector (1,0) rotates with a speed ω=-4/sec around the point (0,0) and will complete 4 revolutions in time T=2π sec.
Fig.8-9b
Trajectory F(4j1t)=f(t)*exp(-4j1t) as a rotating vector modulated by the function f(t). It will make 2 revolutions in a period of T=2π sec with a break of 1π sec in between. The parameter sc4=0 as an average value for T=2π sec is obvious.
Fig.8-9c
The trajectory of F(4j1t) as a circle drawn by the end of the vector in Fig. 8-9b.
sc4=0
Note
sc4=0 and therefore the harmonic for ω=4/sec does not exist.

Chapter 8.7 Fifth harmonic of a symmetrical even square wave h5(t)=a5*cos(5t).
Chapter 8.7.1 Trajectory F(njω0t) of an even square wave for n=5 and ω0=1/sec, i.e. F(5j1t).
The Z plane rotates at a speed of ω=-5/sec

Fig.8-10
Trajectory F(5j1t) of an even square wave
Fig.8-10a
The radius R=1 as a vector (1,0) rotates with a speed ω=-5/sec around the point (0,0) and will complete 5 revolutions in time T=2π sec.
Fig.8-10b
Trajectory F(5j1t)=f(t)*exp(-5j1t) as a rotating vector modulated by the function f(t).
At time T=2π sec, the radius R=1 stays longer on the right half-plane. Therefore, its average value as a vector will be sc5=(1/5π,0).
Fig.8-10c
The trajectory of F(5j1t) as a circle drawn by the end of the vector in Fig. 8-10b.
Notice the “5/4 turn” text that appears. This should convince you that the F(5j1t) trajectory stays longer on the right half-plane of Z. Otherwise, this part of the trajectory is “heavier”.
Chapter 8.7.2 Fifth harmonic against the background of an even square wave, i.e. c0+h5(t).
Acc. to Fig. 8-1c
c5 is the complex amplitude of the fifth harmonic
c5=2*sc5=(2/5π,0) i.e. a5=2/5π and b5=0
Acc. to Fig. 8-1e
h5(t)=(2/5π)*cos(5t)≈0.127cos(5t)

Fig. 8-11
c0+h5(t)=0.5+(2/5π)*cos(3t)
That is, the fifth harmonic with a constant component c0 against the background of a square wave.
Chapter 8.7.3 Fifth approximation of an even square wave, i.e. S5=c0+h1(t)+h3(t)+h5(t).

Fig.8-12
S5(t)=c0+h1(t)+h3(t)+h5(t)
The fifth approximation is more similar to a square wave than the third one in Fig.8-8

Chapter 8.8 Sixth harmonic of an even symmetric square wave, or rather
its lack because c6=0 –>h6(t)=b6*cos(6t)=0.
Chapter 8.8.1 Trajectory F(njω0t) of an even square wave for n=6 and ω0=1/sec, i.e. F(6j1t).

Fig.8-13
Trajectory F(6j1t) of an even square wave
Fig.8-13a
The radius R=1 as a vector (1,0) rotates at a speed ω=-6/sec around the point (0,0) and will complete 6 revolutions in time T=2π sec.
Fig.8-13b
Trajectory F(6j1t)=f(t)*exp(-6j1t) as a rotating vector modulated by the function f(t). It will make 2×1.5 revolutions in a period of T=2π sec with a break of 1π sec in between.
Fig.8-13c
The trajectory of F(6j1t) as a circle drawn by the end of the vector in Fig. 8-13b.
sc6=0
Note
sc6=0 and therefore the harmonic for ω=6/sec does not exist.

Chapter 8.9 Seventh harmonic of an even square wave h7(t)=a7*cos(7t).
Chapter 8.9.1 Trajectory F(njω0t) of an even square wave for n=7 and ω0=1/sec, i.e. F(7j1t).
The Z plane rotates at a speed of ω=-7/sec

Fig.8-14
Trajectory F(5j1t) of an even square wave
Fig.8-14a
The radius R=1 as a vector (1,0) rotates with a speed ω=-7/sec around the point (0,0) and will complete 7 revolutions in time T=2π sec.
Fig.8-14b
Trajectory F(7j1t)=f(t)*exp(-7j1t) as a rotating vector modulated by the function f(t).
At time T=2π sec, the radius R=1 stays longer on the left half-plane. Therefore, its average value will be sc7=(-1/7π, 0).
Fig.8-14c
The trajectory of F(7j1t) as a circle drawn by the end of the vector in Fig. 8-17b.
Notice the words “1 and 3/4 turns” that appear. This should convince you that the F(7j1t) trajectory stays longer on the left half-plane Z. Otherwise, this part of the trajectory is “heavier”.
Chapter 8.9.2 The seventh harmonic against the background of an even square wave, i.e. c0+h7(t).
Acc. to Fig. 8-1c
c3 is the complex amplitude of the third harmonic
c7=2*sc7=(-2/7π,0) i.e. a7=-2/7π and b7=0
Acc. to Fig. 8-1e
h7(t)=-(2/7π)*cos(7t)≈-0.091cos(7t)

Fig. 8-15
h7(t)+0.5, i.e. the seventh harmonic with a constant component c0 against the background of a square wave.
Chapter 8.9.3 The seventh approximation of an even square wave, i.e. S7=c0+h1(t)+h3(t)+h5(t)+h7(t).

Fig.8-16
S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)
The seventh approximation is more similar to a square wave than the fifth in Fig.8-12

Chapter 8.10 The eighth harmonic of an even square wave, or rather its lack because c8=0 –>h8(t)=b8*cos(8t)=0.
Chapter 8.10.1 Trajectory F(njω0t) of an even square wave for n=8 and ω0=1/sec, i.e. F(8j1t).

Fig.8-17
Trajectory F(8j1t) of an even square wave
Fig.8-17a
The radius R=1 as a vector (1,0) rotates at a speed ω=-8/sec around the point (0,0) and will make 8 revolutions in time T=2π sec.
Fig.8-17b
Trajectory F(8j1t)=f(t)*exp(-8j1t) as a rotating vector modulated by the function f(t). It will make 4 revolutions in a period of T=2π sec with a break of 1π sec in between.
Fig.8-17c
The trajectory of F(8j1t) as a circle drawn by the end of the vector in Fig. 8-17b.
sc8=0
Conclusion
sc8=0 and therefore the harmonic for ω=8/sec does not exist.

Chapter 8.11 Remaining harmonics of an even square wave, i.e. for n=9,10,11…∞
We noticed that the centroids scn of the trajectories approach scn=(0,0) as ω increases. In addition, scn of even harmonics are zero. This means that the harmonics decrease with increasing frequency and for an infinitely high pulsation ω, the harmonic amplitudes are zero, i.e. they disappear.
The animation of Fig.8-16 shows that for n=7 the sum of S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t).
And when the number of harmonics is infinitely large, i.e. n=∞
Then the sum of these harmonics
S∞(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)+h9(t)+…+h∞(t)
is the ideal square wave f(t) in Fig. 8-1.