Fourier Transform
Chapter 7. Fourier Transform accounting
Chapter 7.1 Introduction
My main goal was to understand the very idea of the Fourier Transform and that it is sort of a continuous version of the Fourier Series. The Fourier Series applies to successive harmonics of periodic functions f(t) with pulsation ω0=2π/To, which in the complex version are complex coefficients c(n):
–c(0) is a constant component
–c(1), c(2)…c(n) are the amplitudes of complex harmonics with pulsations 1ω0, 2ω0… nω0…
Amplitudes and phases are directly visible in c(1), c(2)…c(n).
The Fourier Transform is concerned with non-periodic functions f(t). We treat it as a function with period To=∞. This leads to some strange things. The constant component and all harmonics are infinitesimal. We take them as zero, although they exist! The transition of one harmonic into another is continuous, so instead of a specific c(ω) we have their average in the range ω-dω…ω…ω+dω. This average is the density of complex amplitudes c(ω)/dω. More precisely, the Fourier Transform is 2π*c(ω)/dω. In this chapter, we will show you how to compute Fourier Transforms of non-periodic functions by definition. So as it is usually done*, not by Fourier Series when To=∞. We did this earlier in Chapters 4 and 6 using Fourier Series, assuming period To=∞. The results should be identical.
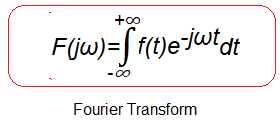
Fig.7-1
Fourier Transform formula
Calculation of transforms is facilitated by various formulas derived from the above definition. Some convolutions of functions, residua, etc. Also transforms of integrals, derivatives, functions shifted in time. Accounting matters, however, are not the main focus of this article.
Chapter 7.2 Fourier Transform of a single square wave pulse
Fig.7-2
Function f(t) as a single wavepulse A=1sec at time t=-0.5sec…+0.5sec
We will compute the transform F(jω) of f(t) using the formula in Fig.7-1.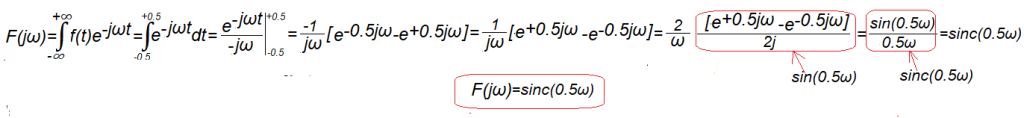
Fig.7-3
Calculation of the transform F(jω) of the function f(t) from Fig.7-2
Integration interval in the range t=-0.5…+0.5. In the remaining range, i.e. t=-∞..-0.5 and t=+0.5…+∞, the integrand function is zero and has no effect on the value of the integral. Don’t be surprised that at some point a rather complicated quotient of complex numbers will turn into a decent real function sin(0.5ω). Well, that’s the math, and if you don’t believe it, check it out with WolframAlpha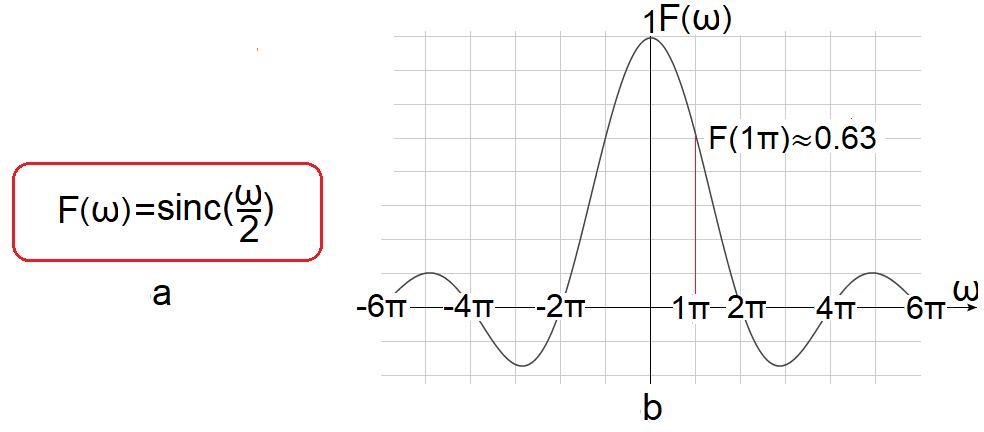
Fig.7-4
Fourier Transform F(jω) of the function f(t) from Fig.7-3
How to treat e.g. F(1π)≈0.63? You already know well that although the amplitude for ω=1π/sec exists, it is infinitely small, with some reluctance you can say that it is zero. However, it changes continuously and in the range of e.g. 1π/sec-dω…+1π/sec…1π/sec+dω its average value relative to ω is F(1π)≈0.63. The result is, of course, the same as in Fig. 4-3 in chapter 4. There we treated f(t) as periodic with To=∞ and therefore we could use the Fourier Series formulas. Thenote also applies to chapter 7.3. Recall that f(t) is an even function, and therefore its transform F(jω) is a real function that can be represented as an ordinary graph.
One more thing. The expression F(jω) and F(ω) can be used interchangeably. Either way, the result is a complex function that can also be real, as in Fig. 7-4.
Chapter 7.3 Fourier transform of the function t=exp(-t) in the interval t=0…+∞
So like in chapter 6
Fig.7-5
Function f(t)as exponential exp(-t)in the intervalt=0…+∞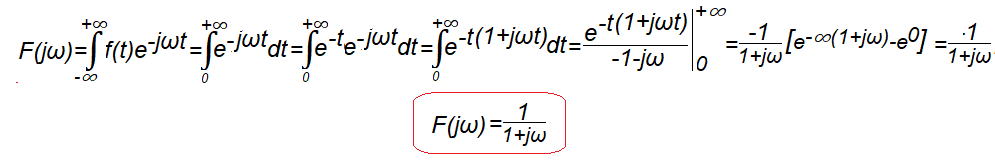
Fig.7-6
Calculation of the transform F(jω) of the function f(t) from Fig.7-5
It is not an even function and therefore its transform is a fully complex function..
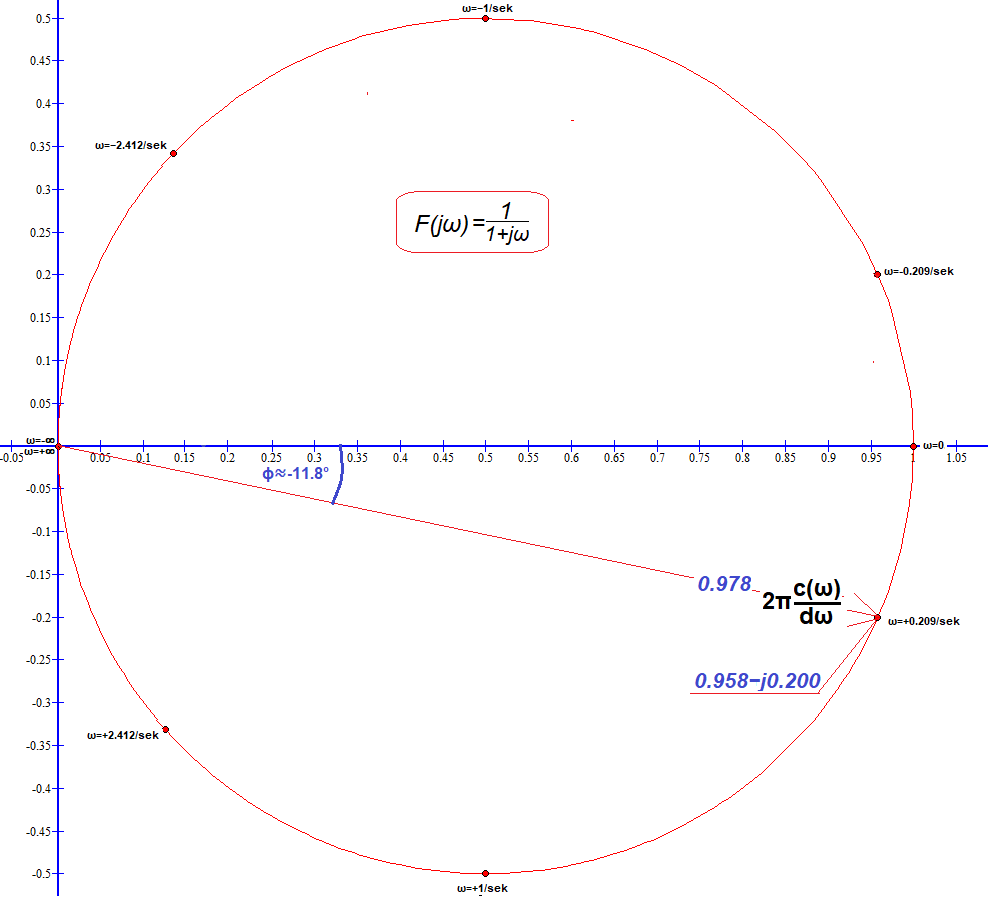
Fig.7-7
Plot of the transform F(jω)=1/(1+jω)
For ω=+0.209/sec, we computed F(+0.209)=1/(1+j0.209)≈0.209-j0.200=0.978*exp(-j11.8º) as the red vector. How? For example, inserting 1/(1+0.209i) into the window. at https://www.wolframalpha.com. We also calculated F(ω) from the formula for ω=-2.412/sec-1/sec,+1/sec and +2.412/sec, these complex numbers are marked with red dots. And ω=+∞,-∞? Here we assumed ω=+1000,-1000 as “almost” infinity. As expected, F(jω)≈0. Needless to say, all values of F(jω) for ω=-∞…+∞ form a circle.
