Complex Numbers
Chapter 2 Arithmetic of complex numbers
Chapter 2.1 Definition
A complex number z, as the name suggests, is a complex (set) of 2 numbers. It consists of a real and imaginary part. It can be represented equivalently as a pair or as a sum. E.g. z=(3,2) or z=3+2j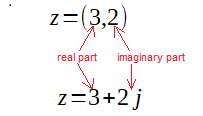
Fig. 2-1
Equivalent notations for the complex number z
While the real numbers can be represented on one real x axis, complex numbers require a plane with the real axis Re z and the imaginary axis Im z. So it’s a bit like a vector, but only similar!
Let’s see what some typical complex numbers z1,… z9 look like.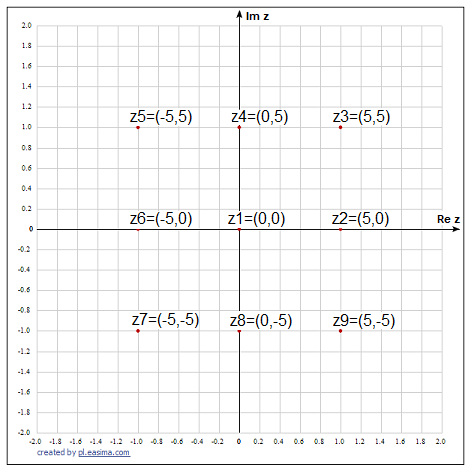
Fig. 2-2
Several typical complex numbers in the z-plane as pairs.
They can also be represented equivalently as sums, e.g. z3=(5,5) is the same as z3=5+j5. Notice that the complex numbers z6, z1, and z2 have only a real part. So these are ordinary real numbers -5,0,+5.
Chapter 2.2 The most “absurd” assumption for complex numbers
Note the quotation marks in the title. Maybe absurd, but not that much.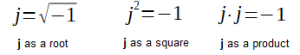
Fig. 2-3
Equivalent definitions of the imaginary number j
1. The imaginary number j is the square root of -1
2. The square of the imaginary number j is equal to -1
3. The product of 2 imaginary numbers j is equal to -1
For something like this in elementary and even high school, you can get your hands slapped! However, it turns out that making such an assumption makes calculations in the real world much easier! Causes 2 complex numbers to be rotated when multiplying. In combination with addition, this facilitates operations on sine waves. And sine waves are electrical engineering!
In it, resistance, induction and capacitance:
– change the amplitude of the current sine wave
– they move the sine wave of the current
relative to the voltage sine wave.
The amplitude and shift of the current can also be calculated using simple trigonometry, but the formulas are then very complicated compared to formulas based on complex numbers.
Note:
Mathematicians use the symbol i, electricians use the symbol j.
Chapter 2.3 Basic operations on complex numbers
Addition
The real component of the sum is equal to the sum of its components. It’s the same with the imaginary component.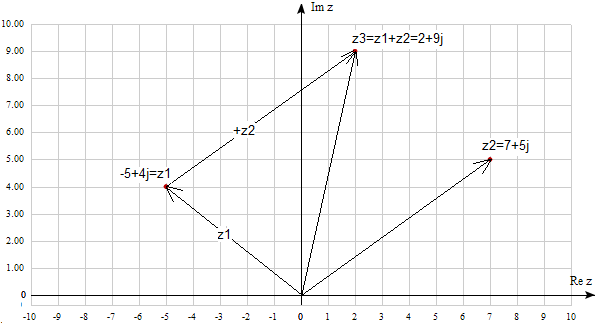
Fig. 2-4
z3=z1+z2
z3=(-5+4j)+(7+5j)=-5+4j+7+5j=2+9j
Notice that in the addition operation, complex numbers behave like vectors.
Subtraction
The real component of the difference is equal to the difference of its components. It’s the same with the imaginary component.
Subtraction can also be treated as adding the opposite number, i.e. -z.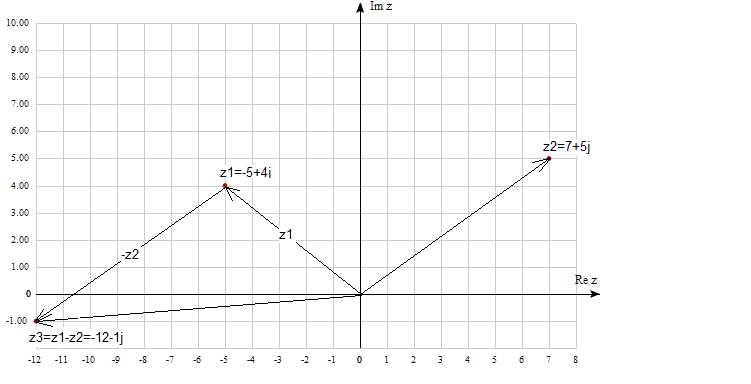
Fig. 2-5
z3=z1-z2
z3=(-5+4j)-(7+5j)=-5+4j-7-5j=-12-1j
Multiplication
Same as multiplying binomials, e.g. (1+x)(2+y)=2+y+2x+2xy. Just remember the “absurd” rule j*j=-1.
Example
z1=0.4+1.6j
z2=1-0.8j
z3=z1*z2=(0.4+1.6j)*(1-0.8j)=0.4+0.32j+1.6j-1.28j*j=1.68+1.28j
It turns out that the multiplication of complex numbers is their rotation!
This is easier to see if we represent a complex number as a vector of length |z| and slope α. In other words, a complex number with module |z| and argument α.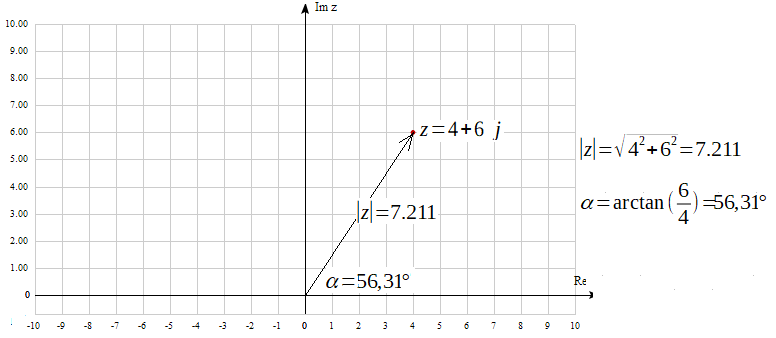
Fig. 2-6
A complex number as a modulus |z| and angle argument α
Here z=4+6j –>tgα=6/4–>α=arctan(6/4)=56.31º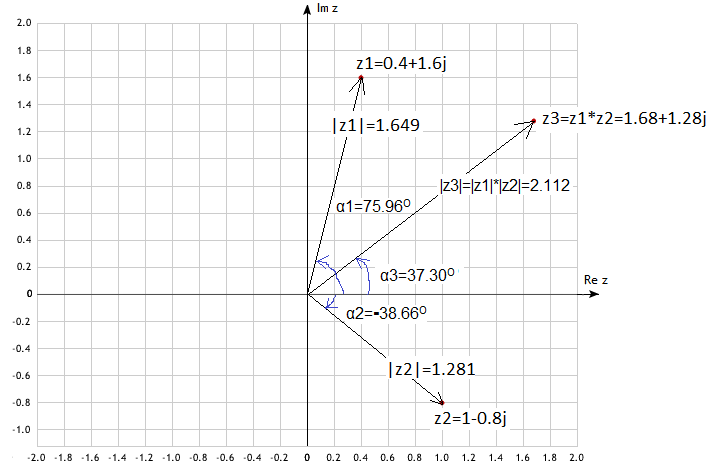
Fig. 2-7
We will not prove it, but from ordinary trigonometry it follows that the product z1*z2 is a number z3 whose modulus and argument are:
|z3|=|z1|*|z2|
α3=α1+α2
Both notations of the number z=a+jb and |z| and α are equivalent, i.e. they show the same number z on the plane of complex numbers.
Sometimes the first save is more convenient, and sometimes the second.
Note that: j*1=1, j*j=-1, j*(-1)=-j and j*(-j)=1
And this is nothing more than successive rotations of the number by 90º of the number 1 when multiplying it by j.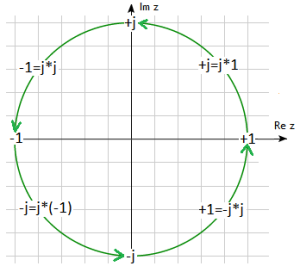
Fig. 2-8
Successive rotations of the number 1
Here, for example, it is clear that -1 is another 2 turns of the number +1.
So -1=j*j*(+1)!
Dividing
We will use a trick. Multiply the numerator and denominator by the so-called conjugate number. The new denominator will always be a real number.
So the main job is to multiply the denominator.
Example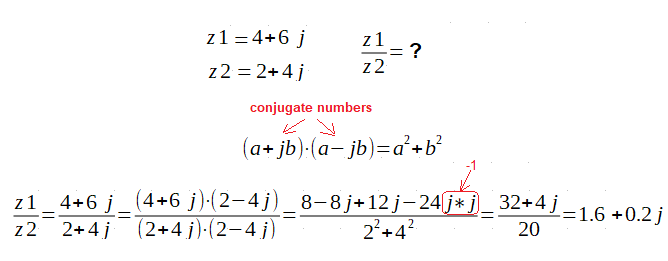
Fig. 2-9
How to divide z1 by z2?
By the way, you learned what conjugate numbers are and what is their product. Not only is it a real number, it’s easy to count! Try to prove it.
When multiplying, the product changes its modulus and rotates according to the formula:
|z3|=|z1|*|z2|
α3=α1+α2
There is also rotation when dividing, but in the opposite direction and the analogous formula looks like this:
|z3|=|z1|/|z2|<–quotient
α3=α1-α2
i.e. we divide the modules and subtract the angle arguments.
Note
α3 positive is a positive rotation, i.e. counter-clockwise motion.
