Rotating Fourier Series
Chapter 6. How to filter out the harmonics with
f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)?
Chapter 6.1 Introduction
The further into the forest, the more… In Chapter 4, we extracted from the function f(t)=0.5*cos(4t) the harmonic 0.5*cos(4t). It’s a bit like pulling a rabbit out of a bag with only one rabbit in it – harmonic 0.5*cos(4t). A cliché, but it was just an excuse to learn the rotating plane method. In Chapter 5 there is a more interesting function f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). The extraction made more sense. There are 2 or even 3 rabbits in the bag – two harmonics and also a constant component c0=+1.3. Now we have a bag with 4 rabbits. The f(t) function has three harmonics and a constant component c0=+0.5. In addition, harmonics are cosines with phase shifts ϕ!
Chapter 6.2 How to extract harmonics from a function using a plane rotating at ω=n*ω0
f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)?
Chapter 6.2.1 Introduction
We will check the rotating function F(jnω0t) at different speeds n*ω0 for n=0…8 and ω0=1/sec. Our goal is to extract the constant component c0=0.5 and three harmonics. We know f(t) as a formula, so we know c0 and 3 harmonics. Let’s assume that “Someone” knows only the time chart in Fig. 6-1b. So what? All that’s left is a rotating plane.
The f(t) function has 3 equivalent forms:
1. f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)
2. f(t)=0.5+0.9*cos(1t)+0.6*sin(1t)+0.6*cos(3t)-0.4*sin(3t)+0.4*cos(5t)+0.2*sin(5t)
3. f(t)=Re {0.5+(0.9-j0.6)*exp(+j1t)+(0.6+j0.4)*exp(+j3t)+(0.4-j0.2)*exp(+ j5t)}
Ad 1. f(t) as in the chapter title.
Ad 2. f(t) where each harmonic was broken down into sine and cosine components.
Ad 3. This is the real part (“Re”) of the complex function (what is between the braces { }
Associate the appropriate coefficients, e.g. (0.9-j0.6)*exp(+j1t) with cos(1t)+0.6*sin(1t) from Ad. 2.
Time chart f(t) in Fig. 6-1b was created on the basis of Ad. 1. Based on Ad. 2 and Ad. 3 would of time chart be the same.
Chapter 6.2.2 Trajectory F(0j1t)=f(t)*exp(-0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45* cos(5t-26.6°) i.e. no rotating
The radius R does not rotate, but changes in Fig. 6-1a along the real axis Re z acc. periodic function
R(t)=F(0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°).
So the trajectory in the complex Z plane in Fig. 6-1a will be a pulsating line.
Fig. 6-1
Function f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°) in complex and real version
Fig. 6-1a
F(0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°) in the complex version.
Fig.6-1b
F(0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°) in the real version, i.e. the time chart f(t).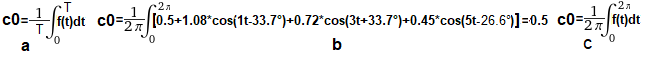
Fig.6-2
The formula for the constant component of the periodic function f(t), i.e. c0 of the Fourier Series
This is the average of the function f(t) in period T
Fig.6-2a
General formula for f(t) with period T
Another look at c0=0.5. It is also the centroid sc0=(0.5,0) of the “rocking” trajectory in Fig. 6-1a.
Fig.6-2b
The formula for our f(t) when T=2π.
Fig.6-2c
The formula for any f(t) when T=2π.
Chapter 6.2.3 Trajectory F(1j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-1j1t)
i.e. with rotating 1ω0=-1/sec
In this and the following subsections, the pulsating radius R(t) from Fig. 6-1a will begin to spin at speeds -1/sec … -8/sec. Here the animation will last T=2π/ω0≈6.28sec and radius R=0.5 from Fig.6-3a will make 1 rotation. At the next rotation speeds, i.e. -ω0=-2/sec, -3ω0=3/sec…-8ω0=-8/sec, the time of each animation will also be T≈6.28sec. This means that the radius R=0.5* will make 2.3…8 turns. Or in other words, the complex plane Z will make 2.3…8 revolutions.
*Note
I chose R=0.5 as the reference radius of the rotating plane. By chance, the constant component is also c0=0.5
Fig. 6-3
F(1j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-1j1t)
Fig. 6-3a
Radius R=0.5 1ω0=-1/sec will make 1 rotation
Fig.6-3b
During rotation, the length of the radius changes according to the function
R(t)=f(t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°).
So the complex function F(1j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-1j1t) is realized
Fig.6-3c
Complex function F(1j1t) as a trajectory.
Trajectory F(1j1t) orbits around the centroid sc1=(0.45,-0.3) with a speed of 1ω0=-1/sec. It is a vector and can also be written in exponential form sc1=0.54*exp(j-33.7°). In Chapter 7, you will learn that with sc1=(0.45,-0.3), otherwise sc1=0.54*exp(-j33.7°), you can easily read the first harmonic of the function as 1.08*cos(1t-33.7°) or 0.9* cos(1t)+0.6*sin(1t).
Chapter 6.2.4 Trajectory f(2j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-2j1t)
i.e. with spinning 2ω0=-2/sec
Fig.6-4
F(2j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-2j1t) .
Fig. 6-4a
The radius R=0.5 will make 2 revolutions.
Fig.6-4b
The complex function F(2j1t) as a rotating vector
Fig.6-4c
Complex function F(2j1t) as a trajectory.
The centroid of the trajectory F(2j1t) is sc2=(0,0). So the function f(t) has no harmonic with pulsation 2ω0=2/sec. This zero sc2 is not very convincing. It seems like it should be slightly shifted to the right. Note, however, that the speed of the trajectory on the left is on average lower than on the right.
Chapter 6.2.5 TrajectoryF(3j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-3j1t)
i.e. with spinning 3ω0=-3/sec
Fig.6-5
F(3j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-3j1t).
Fig.6-5a
The radius R=0.5 will make 3 turns.
Fig.6-5b
The complex function F(3j1t) as a rotating vector.
Fig.6-5c
Complex function F(3j1t) as a trajectory.
The trajectory F(3j1t) revolves around sc3=(0.3,0.2) with a speed of 3ω0=-3/sec. It is a vector and can also be written in exponential form sc3=0.36*exp(+j33.7°). In Chapter 7, you will learn that from the centroid sc3=(0.3,0.2) or sc3=0.36*exp(+j33.7°) you can easily read the third harmonic of the function as 0.72*cos(3t+33.7°) or 0.6*cos( 3t)-0.4*sin(3t).
Chapter 6.2.6 Trajectory F(4j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-4j1t)
i.e. with rotation 4ω0=-4/sec
Fig.6-6
F(4j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-j26.6°)]*exp(-4j1t)
Fig. 6-6a
The radius R=0.5 will make 4 turns.
Fig.6-6b
The complex function F(4j1t) as a rotating vector
Fig.6-6c
Complex function F(4j1t) as a trajectory.
The centroid of the trajectory F(4j1t) is sc4=(0,0). So the function f(t) has no harmonic with a pulsation of 4ω0=4/sec.
As in Fig. 6-4c, the centroid sc4=(0,0) seems too shifted to the left.
Chapter 6.2.7 Trajectory F(5j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-j26.6°)]*exp(-5j1t )
i.e. with rotating 5ω0=-5/sec
Fig. 6-7
F(5j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-j26.6°)]*exp(-5j1t).
Fig.6-7a
The radius R=0.5 will make 5 revolutions.
Fig.6-7b
The complex function F(5j1t) as a rotating vector.
Fig.6-7c
Complex function F(5j1t) as a trajectory.
The trajectory F(5j1t) revolves around sc5=(0.2,-0.1) with a speed of 5ω0=-5/sec. It is a vector and can also be written in exponential form sc5=0.36*exp(+j33.7°). In Chapter 7, you will learn that from the centroid sc5=(0.2,-0.1) or sc5=0.36*exp(-j26.6°) you can easily read the fifth harmonic of the function as 0.45*cos(5t-33.7°) or 0.4*cos (5t)+0.2*sin(5t).
Chapter 6.2.8 Trajectory F(6j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-6j1t)
i.e. with rotation 6ω0=-6/sec
Fig.6-8
F(4j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-6j1t)
Fig. 6-8a
The radius R=0.5 will make 6 turns.
Fig.6-8b
The complex function F(6j1t) as a rotating vector
Fig.6-8c
Complex function F(6j1t) as a trajectory.
The centroid of the trajectory F(6j1t) is sc6=(0,0). So the function f(t) has no harmonic with a pulsation of 6ω0=6/sec.
Chapter 6.2.9 Trajectory F(7j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-7j1t)
i.e. with spinning 7ω0=-7/sec
Fig.6-9
F(7j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-7j1t)
Fig. 6-9a
The radius R=0.5 will make 7 revolutions.
Fig.6-9b
The complex function F(7j1t) as a rotating vector
Fig.6-9c
Complex function F(7j1t) as a trajectory.
The centroid of the trajectory F(7j1t) is sc7=(0,0). That is, the function f(t) has no harmonic with a pulsation of 7ω0=7/sec.
Chapter 6.2.10 Trajectory F(8j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-8j1t)
i.e. with rotation 8ω0=-8/sec
Fig.6-10
F(8j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-8j1t)
Fig. 6-10a
The radius R=0.5 will make 8 turns.
Fig.6-10b
The complex function F(8j1t) as a rotating vector
Fig.6-10c
Complex function F(8j1t) as a trajectory.
The centroid of the trajectory F(8j1t) is sc8=(0,0). That is, the function f(t) has no harmonic with a pulsation of 8ω0=8/sec.
