Rotating Fourier Series
Chapter 5. How to filter out the harmonics with 1.3+0.7*cos(2t)+0.5*cos(4t)?
Chapter 5.1 Introduction
In the previous chapter, we extracted the harmonic 0.5*cos(4t) from the function f(t)=0.5*cos(4t) and from the function f(t)=0.5*cos(4t-30°) using a rotating speed of ω=n*ω0 Z planes. Now we will do the same, but with the function f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). The pulsations of both cosines are different! I wonder how this will affect the f(t) plot and the rotating trajectories F(jnω0t)?
You will find that:
– regardless of the nω0 pulsation, the trajectory period F(jnω0t) is T=6.28 sec
– for ω=0 the function does not rotate!
– for ω=1*ω0=1/sec…8*ω0=8 the radius R=1 will make 1…8 turns
Will it be possible to extract the constant component c0=1.3 and the harmonics h2(t)=0.7*cos(2t) and h4(t)=0.5*cos(4t)?
Chapter 5.2 Trajectory F(0j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-0j1t) i.e. no rotation
A problem similar to Fig. 4-2 of the previous chapter. The radius R does not rotate, but changes according to periodic function R(t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). So the trajectory in the complex plane Z is
F(0j1t)=f(t)*exp(-j0)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). By the way, you will see the time chart of the f(t) function.
Fig. 5-1
Function F(0j1t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) in complex and real version
Fig. 5-1a
F(0j1t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) in complex version
Fig. 5-1b
F(0j1t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) in real version
Conclusion.
The average value of f(t) over the period T=2π≈6.28sec (and also T=πsec≈3.14sec) is c0=1.3.
It is also the centroid sc0=(1.3,0) of the “rocking” trajectory in Fig.5-1a when the plane rotation speed ω=0. Another name for parameter c0=1.3 is the constant component of f(t).
Note.
In the Fourier Series of the periodic function f(t) the first element is the constant component – coefficient c0=a0. This is the average f(t) over period T.
We calculate it as an integral from the formula below.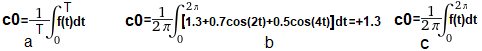
Fig.5-2
The formula for the constant component of the periodic function f(t), i.e. for c0
This is the average of f(t) over period T
Fig.5-2a
General formula for f(t) with period T
Fig.5-2b
Formula for f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) and T=2π
Fig.5-2c
Formula for any f(t) and T=2π
Chapter 5.3 Trajectory F(1j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-1j1t) i.e. with rotation 1ω0=-1/sec
The radius R=1 rotates with 1ω0=-1/sec.
See the animation in Fig. 5-1a. The end of the vector moves “back and forth” around c0=(+1.3, 0) by formula R(t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). What if the vector started rotatimg at 1ω0=-1/sec? So “clockwise” and with a period of T≈6.28sec. Then its motion in the complex plane Z is described by the complex function F(1j1t).
Fig.5-3
F(1j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j1t)
The animation takes T=2π/ω0≈6.28sec.
Fig.5-3a
Radius R=0.5 with 1ω0=-1/sec will make 1 revolution.
Notice that we chose R=0.5 as the reference constant radius. Also in the next animations
Fig.5-3b
During the rotation, the length of the radius changes according to the function R(t)= f(t)=1.3+0.7*cos(2t)+0.5*cos(4t).
So the complex function is implemented as a rotating vector F(1j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j1t)
Fig.5-3c
Complex function F(1j1t) as a trajectory.
It is drawn by the vector from Fig.5-3b. The centroid of the trajectory F(1j1t) is evidently sc1=(0,0)=0. So function f(t) has no harmonic with pulsation 1ω0=1/sec.
Chapter 5.4 Trajectory F(2j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-2j1t) i.e. with rotation 2ω0=-2/sec
Fig.5-4
F(2j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-2j1t)
The animation lasts T≈6.28sec.
Fig. 5-4a
Radius R=0.5 will make 2 revolutions.
Fig.5-4b
The complex function F(2j1t) as a rotating vector.
The variable-length vector R(t) will make 2 rotations.
Fig.5-4c
The complex function F(2j1t) as a trajectory.
Second rotation on the same track. The centroid of the trajectory is now sc2=(0.35,0). It is a vector and can also be written in the complex exponential form sc2=R*exp(jϕ)=0.35*exp(j0°). In Chapter 7 you will learn that from the centroid of the trajectory you can easily read the 2nd harmonic of f(t) as h2(t)=0.7cos(2t). Look at f(t). Correct!
Note.
Don’t go into how we calculated the centroid sc2=(0.35,0). Trust your intuition for now, although it seems like it should be a bit more to the right. Note, however, that the velocity of the left side of the trajectory is slightly slower. So the distances from sc2 will be a little more densely spaced than on the right side. As if the trajectory was drawn with a thicker line here.
Chapter 5.5 Trajectory f(3j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-3j1t) i.e. with spin 3ω0=-3/sec
Fig.5-5
F(3j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-3j1t)
The animation lasts T≈6.28sec.
Fig. 5-5a
The radius R=0.5 will make 3 revolutions.
Fig.5-5b
The complex function F(3j1t) as a rotating vector
Fig.5-5c
Complex function F(3j1t) as a trajectory.
The centroid of the trajectory F(3j1t) is sc3=(0,0)=0. So the function f(t) has no harmonic with pulsation 3ω0=3/sec.
Chapter 5.6 Trajectory F(4j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-4j1t) i.e. with spin 4ω0=-4/sec
Fig.5-6
F(4j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-4j1t)
The animation lasts T≈6.28sec.
Fig. 5-6a
The radius R=0.5 will make 4 turns.
Fig.5-6b
The complex function F(4j1t) as a rotating vector.
The variable-length vector R(t) will make 4 rotations.
Fig.5-6c
Complex function F(4j1t) as a trajectory.
3rd and 4th rotation along the same track. Non-zero centroid sc4=(0.25,0)!
From the centroid sc4, the 4th harmonic of the f(t) function can be read as 0.5cos(4t).
Chapter 5.7 Rotating radius 5ω0=5/sec, so the trajectory F(j5ω0t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j5ω0t) for 5ω0=-5/sec.
Fig.5-7
F(j5ω0t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j5t)
The animation lasts T≈6.28sec.
Fig. 5-7a
The radius R=0.5 will make 5 revolutions.
Fig.5-7b
The complex function F(5j1t) as a rotating vector
Fig.5-7c
Complex function F(5j1t) as a trajectory.
The centroid of the trajectory F(5j1t) is sc5=(0,0)=0. So the function f(t) has no harmonic with a pulsation of 5ω0=5/sec.
Chapter 5.8 Trajectory F(6j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-6j1t) so with rotation 6ω0=-6/sec
Fig.5-8
F(6j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j2t)
The animation lasts T≈6.28sec.
Fig.5-8a
The radius R=0.5 will make 6 turns.
Fig.5-8b
The complex function F(6j1t) as a rotating vector
Fig.5-8c
Complex function F(6j1t) as a trajectory. 3 revolutions along the same path, which is why it seemingly stopped.
The centroid of the F(6j1t) trajectory is sc6=(0,0)=0*. So the function f(t) has no harmonic with a pulsation of 6ω0=6/sec.
*sc6=(0,0) is not as obvious as, for example, for Fig.5-7c. It seems too far to the left. Note, however, that the trajectory velocities on the left are lower than those on the right.
Chapter 5.9 Trajectory F(7j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-7j1t) i.e. with spin 7ω0=-7/sec
Fig.5-9
F(7j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-7j1t)
Complex function F(j7ω0t) for 7ω0=7/sec.
The animation lasts T≈6.28sec.
Fig. 5-9a
The radius R=0.5 will make 7 revolutions.
Fig.5-9b
The complex function F(7j1t) as a rotating vector
Fig.5-9c
Complex function F(7j1t) as a trajectory.
The centroid of the trajectory F(7j1t) is sc7=(0,0)=0. So the function f(t) has no harmonic with a pulsation of 7ω0=7/sec.
Chapter 5.10 Trajectory F(8j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-8j1t) i.e. with spin 8ω0=-8/sec
Fig.5-10
F(8j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-8j1t)
The animation lasts T≈6.28sec.
Fig. 5-10a
The radius R=0.5 will make 8 turns.
Fig.5-10b
The complex function F(8j1t) as a rotating vector.
Fig.5-10c
Complex function F(8j1t) as a trajectory.
The centroid of the trajectory F(8j1t) is sc8=(0,0)=0. So the function f(t) has no harmonic with a pulsation of 8ω0=8/sec.
