Fourier Series Classically
Chapter 1 Introduction
Chapter 1.1 Introduction
It is also an introduction to the next courses “Fourier Transform” and “Laplace Transform”. The latter will appear in the future.
Chapter 1.2 Any time function f(t) can be decomposed into sine waves!
Maybe not every*, but let’s not be petty. It is easiest when we are dealing with periodic functions f(t) lasting from minus to plus infinity as in Fig. 1-2.c. This is where the Fourier Series comes in.
And when the function runs in finite time, e.g. a single rectangular pulse? Or in infinite time but the energy of the pulse is finite, e.g. discharge voltage of the RC system. This is what the Fourier Transform course, which can be found on the main page.
And when the function runs in infinite time and has infinite energy, e.g. a unit step or a quadratic function? Here is a job for the Laplace Transform, which will appear on this website someday..
Note
Fourier Series, Fourier Transform or Laplace Transform decomposes almost any* function f(t) into a sum of sine waves with different frequencies, amplitudes and phase shifts!
* except for this type of freaks.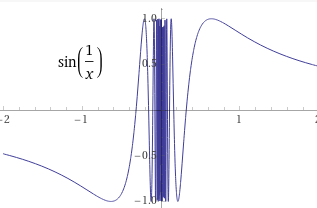
Fig. 1-1
A function that is not subject to Series or Fourier or Laplace Transform.
Fortunately, such functions are rarely associated with real physical phenomena.
Chapter 1.3 Trigonometric Fourier Series
The periodic function f(t) can be approximated by a FourierSeries.
Here f(t) is just a function of time t, but it could just as well be a function of position x, which is f(x).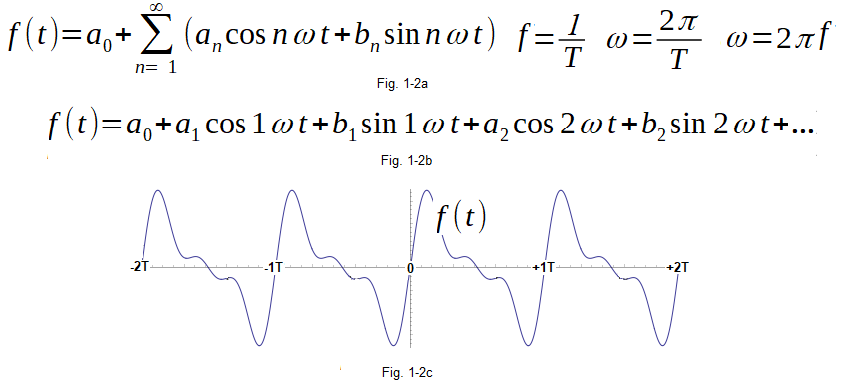
Fig.1-2
Trigonometric decomposition of the periodic function f(t) into a Fourier Series.
Note:
For descriptions of alternating currents, the frequency f is used as the reciprocal of the period T, or the so-called pulsations–>angular velocity ω. The frequency f is used by ordinary people, e.g. f=50 Hz, while the pulsation ω is intended for electricians. Thanks to this, the formulas are a little shorter, because instead of 2πf we have only ω.
Fig. 1-2a
Formula using sum-sigma sign
Fig. 1-2b
The formula without this sigma, which is perhaps clearer. The ω pulsation of the first harmonic is better seen here. The pulsations of successive harmonics are their multiples. The coefficients a1,b1,a2,b2… are the amplitudes of the successive sine/cosines. These are constants e.g. a1=1 ,b1=-0.5,a2=0 ,b2=1.25,a3=0.1, … which we will discuss in Chapter 2.
Fig. 1-2c
An example of a periodic function f(t) with period T=2π sec corresponding to the pulsation ω=1/sec.
The above formulas are most often accurate for n=∞. The value of n can also be finite, e.g. n=3 in Fig. 2-3 in Chapter 2.
Chapter 1.4 Complex Fourier Series
It’s just aotherwise written Trigonometric Fourier Series.
At first, they were less understandable, because some complex numbers instead of good real ones. But many things calculate easier. Not only that, it’s more intuitive! Especially after watching the animation. You will notice, for example, an analogy to the Solar System, in which the Earth revolves around the Sun, the Moon revolves around the Earth, etc… More on this in Chapter 3.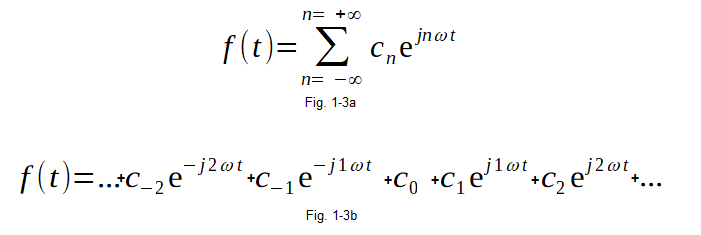
Fig. 1-3
Complex decomposition of the periodic function f(t) into a Fourier Series.
Fig. 1-3a The sum-sigma formula
Fig. 1-3b Formula without this sign. Probably more transparent. The formulas are clearly simpler than in Fig. 1-2. Unfortunately, the coefficients cn used are complex numbers. To remind them, see the Complex Numbers course on the home page. Notice that on the right of the equations there is a rather complicated sum of complex numbers, the result of which is the real function f(t)! The imaginary components compensated each other!![]()
Fig. 1-4
Fourier Series coefficients as complex numbers.
Chapter 1.5 What is all this for?
Fourier Series appeared over 200 years ago, but they are also used in our times. And the so-called The Fast Fourier Transform, which is just a digital algorithm for calculating the Fourier Transform, was only published in 1965 by Cooley and Tuckey. What is all this for? It turns out that it is difficult to find a field in which there would be no Series or Fourier Transform.
An example from acoustics. The word “hello” was registered with a microphone as a function of time f(t).
The author is Erik Cheever. By the way, I highly recommend his article https://lpsa.swarthmore.edu/Fourier/Series/WhyFS.html.
Click the sound recorder button. You will hear a not very loud “Hello”.
Fig. 1-5
The word “Hello” written as:
Fig. 1-5a function of time f(t)
For the average bread eater, the physical phenomenon (here the word “hello”) is associated with the f(t) function of time, as in Fig. 1-5a. The function f(t) begins at t=0.1 sec and ends at t=0.6 sec. It is very confusing compared to, for example, a square function. How to analyze it?
Fig.1-5b frequency spectrum F(ω)
The function f(t) of the word “hello” as a sum of specific sinusoids, each of which has its own amplitude, ω pulsation (f frequency in Fig. 1-5b) and φ phase. The graph shows only the amplitudes, so it does not contain the full information about “hello”, but it is clearly simpler than Fig.1-5a. The first benefit of approaching the phenomenon as a frequency distribution, i.e. spectrum F(ω) you will see in the next video. You will hear the same “hello” but with an annoying distortion.
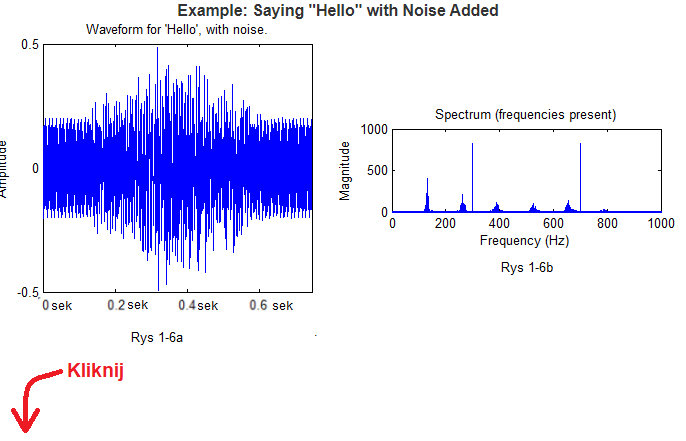
Fig. 1-6
The word “Hello” written as:
Fig. 1-6a function of time f(t)
Note that although the continuous tone disturbance is not very complicated, the timing diagram has changed quite a bit. Where in this tangle to look for disturbance?
Fig.1-6b frequency spectrum F(ω)
The frequency spectrum F(ω) has not changed much compared to Fig. 1-5a. Only 2 additional sinusoidal fringes appeared around 300Hz and 700Hz. Just cut them out and you’ll get a clean “Hello” as before. This notch is precise if we use digital algorithms. In the past, analog filters with coils and capacitances were used, which also cut out the original frequencies, but not so precisely.
I hope you see the benefit of the spectral approach to the function of time.
Chapter 1.6 Other domains with Fourier Series or Transform
Digital image processing
You’ve probably seen a movies in which tsar Nicolas or emperor Francis Joseph II are alive. As if it was made yesterday from a good cell. And it’s all thanks to the Fourier Transform. What is it about? Each image can be decomposed into sinusoids with known parameters. You only need to save them and recreate them as an image at any time. This will usually take less space than remembering every pixel of an image. This is an example where the sine waves refer to the x positioning (strictly xy pozitioning) and not the time t. And most importantly, it is easier to remove the interferences – unnecessary additional sine waves from the imperfect original from more than 100 years ago. Especially when we use Artificial Intelligence. Similar to the sound in Fig.1-6.
Machine Diagnostics
The turbo generator must be perfectly balanced. After all, these are tons of rapidly rotating mass. An ideal machine gives the appropriate spectrum F(ω) for the frequency varying from 0 to the maximum. What if some sawdust got into the shaft? The human ear may not pick it up, but a distinct band will appear in the spectrum. Now finding that sawdust is just a matter of looking closely at the shaft.
Earthquake
Fortunately, this does not apply to all, only some, for example, California residents. The so-called time chart thanks to Mr. Fourier, the seismograph can be broken down into individual harmonics. After a number of years there, it will turn out that certain frequencies predominate. And this is important information for architects. The buildings themselves must suppress them! At certain heights, large swinging masses are appropriate, which, together with the rest of the building, reduce its oscillation amplitudes. Why? Because they’re swinging ini counter-phase with the rest of the building.
Automatics
Control systems with and without feedback are described by differential equations. Fortunately, with some simplifications, these are linear differential equations. The equations will be easier when its solution, i.e. the f(t) function, is decomposed into sinusoidal components. And this is nothing more than a Series , Fourier Transform or Laplace Transform. Why easier. Because the derivative of the sine is cosine and the cosine is sine (with a minus). I will not go into details, but such equations can be converted to quadratic equations or higher degrees. Now we can solve and analyze them using “ordinary” algebra.
Medicine
More than once you’ve been lying on a doctor’s couch connected to monitors with cables.
For the Cardiologist, the graph on the monitor is an electrocardiogram
For a Neurologist, it is an electroencephalogram.
Based on them, an experienced doctor knows more or less what ails you. Experience is gained with practice. Especially since the graphs are not much different. And here is the field for the Fourier Transform, which will break the function f(t) into individual sinusoids–>frequency spectrum. Spectra for different diseases are different. This is where the aforementioned Fast Fourier Transform-FFT comes in handy.
An example of how neurologists go deep into the Fourier Transform is youtube Click.
