Fourier Tranform
Chapter 2 Fourier series of a square wave as a bar diagram
Chapter 2.1 Time chart of a square wave
In the next chapter, we will build the Fourier Transform of the simplest non-periodic function, which is a single rectangular pulse. It is somehow related to the even square wave which we decomposed into a Fourier Series in the chapter 8. The description often includes the concept of the so-called band plot, which is simply a Fourier Series in a graphical version. In this chapter we will show some fringe plots to approximate a square wave with different periods, as the sum S7(t) of its first few harmonics.Fig. 2-1
Fig. 2-1
Square wave with parameters:
A=1-amplitude
ω0=1/sec-pulsation corresponding to the period T=2πsec≈6.28sec.
ϕ=0
50%-duty cycle
The time chart started theoretically at the beginning of the world for t=-∞ in the middle of the pulse when A=1. So for t=0 it will also be half of the pulse. So it is an even function. Similarly to e.g. cosine, which also starts in the “middle”. The left semi-time axis t is not shown.
Chapter 2.2 The seventh approximation of an even square wave, i.e. S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t).
In chapter 8 of the article “Rotating Fourier Series” we calculated the approximation of the even square wave S7(t) when ω0=1/sec—>Fig. 2-3. We calculated the coefficients an at cos(nω0t) as twice the centroids scn of the trajectory F(njω0t) of the function f(t)=even square wave. If you don’t know much about these centroids, we simply calculated the coefficients a(n) of the Fourier Series. We did not take into account the remaining harmonics, i.e. for n>7, which resulted in a “wavy” approximation of s7(t) of the square wave. Even harmonics hn(t) are zero because a(2)=a(4)=a(6)=…0. For n=∞ we would get a perfect square wave from the animation of Fig. 2-1. All Fourier Series coefficients b(n) are zero because f(t) is an even function.
Fig.2-2
S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)
You see in the animation
– an even square wave with period T=2π sec, i.e. ω=1/sec
– its seventh approximation S7(t) as a finite Fourier Series.
– constant component c0=a0=0.5
– harmonics h1(t), h3(t), h5(t) and h7(t).
After substituting the specific parameters ω0, a(1), a(3), a(5) and a(7) from the description above, we will obtain the formula for S7(t) as a Fourier Series approximation of the function f(t).
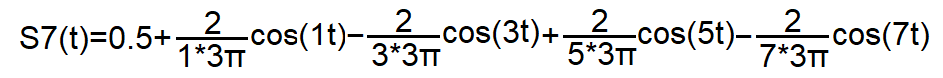
Fig.2-3
The specific formula for the Fourier Series approximation of a square wave in Fig. 2-1.
Chapter 2.3 The single side band bar diagram of a square wave
Single-band, because only for non-negative pulsations.
The most accurate version of the Fourier Series is, of course, its formula itself.
For example, n=7 and an even square wave, it is Fig. 2-3
A less accurate (because it depends on the age and glasses of the observer), but more intuitive version are time charts, e.g. Fig. 2-2. The rectangular function itself, the constant component and the 4 harmonics of the S7(t)
approximation are visible. We see that the components add up to give S7(t).
A bar diagram as an animation, it is the most intuitive. The pulsations ω and the amplitudes a(n) of the harmonics and the constant component a0 are clearly visible. And where is the φ phase? Nowhere. Because the bar diagram is suitable only for the analysis of even functions f(t). These functions have only a real component where either φ=0 (positive bars) or φ=180º (negative bars). So let’s make a bar diagram for S7(t) in Fig. 2-3. That is, for the square wave approximation in Fig. 2-1 when n=7.
Fig. 2-4
Bar diagram of a single side band of a square wave for n=7 and ω=1/sec
More precisely, it is an animation of the formula in Fig. 2-3, and the chart you see in Fig. 2-4 (before animation) is the initial state S7(t), i.e. for t=0. The harmonics hn(t) for ω even pulsations are zero. Otherwise – they do not exist.
1. The animation takes about 3T=3*2π sec≈19sec
2. Harmonic pulsations are placed on the horizontal axis for ω=0…+7/sec.
3. a0=+0.5 the constant component of a square wave, i.e. the bar for ω=0
4. Animation of the first harmonic h1(t) i.e. the bar for ω=1/sec
…
7. Animation of the 7th harmonic h7(t), i.e. a bar for ω=7/sec
8. Sum of S7(t) a0 and 4 harmonics hn(t) i.e. the left extreme bar. Compare with S7(t) in Fig. 2-2. Notice that it is in phase with h1(t). If n=∞, you would see perfect “rectangular” motions without jitter, such as in Fig. 2-1. Without the so-called the Gibbs effect – maximum “swing” at the beginning and end of the impulse.
In the initial state t=0, you see the amplitudes of the harmonics hn(t), which is with the Fourier coefficients a(n) of the square wave in Fig. 2-2. Negative amplitudes for h3(t) and h7(t) means that these are the values at the initial moment for t=0, which results from the formula Fig. 2-3. In other words, φ=180º, because in this phase the cosines h3(t), h7(t), … when t=0 “start”.
The function f(t)=S7(t) on the left side of the graph is at any time the sum of all swinging bars, i.e. the constant component a0 and the 4 harmonics h1(t), h3(t), h5(t) and h7(t ). They “swing” with pulsations ω=n*ω0=n*1/sec, that is with ω=1/sec, 3/sec, 5/sec and 7/sec. The dotted line is the constant component a0=0.5.
I emphasize that the animation with the swinging bars is the most intuitive version of the Fourier Series! You see the sum S7(t), the 4 harmonics hn(t) and the DC component a0. And the Fourier coefficients a(n) themselves are bars at the initial moment. We can formally treat the constant component a0 as a harmonic h0(t) with zero pulsation.
Note:
If the bar graph is so cool and intuitive, why isn’t it used for all periodic functions f(t)? The answer is simple. Because it applies only to functions of even functions for which the Fourier series has no sinusoidal components, i.e. b(n).
Chapter 2.4 The double side band bar diagram of a square wave
The left “negative” semi-axis ω in Fig. 2-4 is, apart from the f(t) line, undeveloped. What a waste!
From trigonometry we know that cos(ωt)=cos(-ωt). So let’s divide each harmonic hn(t) by 2 and divide them into 2 semi-axes of ω. So h+n(t)=h-n(t)=hn(t)/2. So we created a double side band graph of a square wave.
Fig. 2-5
Bar diagram of a double side band of a square wave for n=7 and ω=1/sec.
Each right harmonic h+n(t) band has its symmetric left h-n(t) counterpart.
For obvious reasons
1. a0=+0.5 the constant component of a square wave, i.e. the bar for ω=0 and is the same as a0 for the double-band in Fig. 2-4
2. The remaining harmonics, or “swings”, are the halves of Fig. 2-4
3. f(t) bar is the same as in Fig. 2-4
What’s all this for? You will find that the introduction of negative pulsations will create a certain elegance in the formulas. Even the animation is more aesthetic than Fig. 2-4. Remember the centroids scn of the trajectory F(njω0t) in the article “Rotating Fourier Series”? I was intrigued as to why c(n)=2*scn. Why the complex amplitude of the nth harmonic hn(t), i.e. c(n), is a double scn and not just a (single) scn. That’s what math says. Agreed, but there was a “why?” in the back of my head. Now I know. Because harmonics have to be divided into positive and negative pulsations!
Chapter 2.5 Influence of square wave pulsations on bar diagram graph.
Chapter 2.5.1 Introduction
More precisely, the influence on double-band bar diagrams, because we will only be interested in such. Fig. 2-5 is a double-band bar diagram of the even square wave in Fig. 2-1 with period T=2π sec–>ω=1/sec. If the amplitude were A=2, the graph would be 2 times higher. It is obvious. And period T?
We will examine 2 cases, because the first-T=2π sec–>ω=1/sec is as above–> Fig. 2-5.
– T=4π sec–>ω=0.5/sec
– T=1π sec–>ω=2/sec
Chapter 2.5.2 Square wave bar diagram when T=4π sek–>ω=0.5/sek
Fig. 2-6
Square wave with parameters:
A=1-amplitude
ω0=0.5/sec-pulsation corresponding to period T=4πsec≈12.56sec.
ϕ=0 (phase)
50%-square wave duty cycle
A wave similar to that in Fig. 2-1. Only the smaller pulsation ω0=0.5/sec, i.e. T=4π sec. It will be interesting to see how this affects the bar diagram.
Fig. 2-7
Bar diagram of a double side band of a square wave for n=7 and ω=0.5/sec.
The bars are 2 times slower and 2 times “denser” than in Fig. 2-5.
Chapter 2.5.3 Square wave bar diagram when T=1π sek–>ω=2/sek
Fig. 2-8
Square wave with parameters:
A=1-amplitude
ω0=2/sec-pulsation corresponding to period T=1πsec≈3.14sec.
ϕ=0 (phase)
50%-square wave duty cycle
A wave similar to that in Fig. 2-1. Only the bigger pulsation ω0=2/sec, i.e. T=1π sec. It will be interesting to see how this affects the bar diagram.
Fig. 2-9
Bar diagram of a double side band of a square wave for n=7 and ω=2/sec.
The bars are 2 times faster and 2 times “rarer” than in Fig. 2-5.
Chapter. 2.6 Conclusions
1. Bigger signal–>Higher bars
2. “Wider signal in time”—>The bars are more densely distributed
Looking ahead and generalizing to the Fourier Transform
1. Bigger signal–>Higher transform
2. “Broader in time signal”—>Narrower Transform
