Rotating Fourier Series

Chapter 10. Fourier Series of a square wave with a shift -30º

Chapter 10.1 Introduction

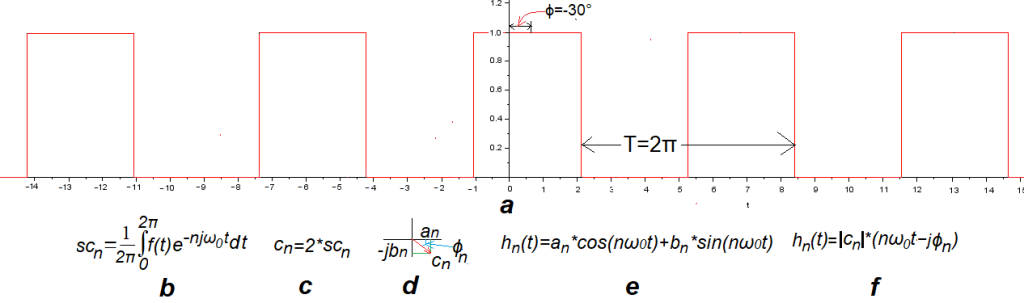
Fig.10-1
Square wave f(t) A=1, ω=1/sec and ϕ=-30° or -π/6.
The parameter ϕ=-30° of the wave means that it is shifted by -30° relative to the even wave from Chapter 8. Therefore, it is not an even or odd function. So bland. The even wave had only cosine harmonics an, i.e. an≠0 i bn=0 components. In turn, the odd one has only sinusoidal components an=0 i bn≠0, i.e. components an=0. We now expect cosine and sine components to occur i.e. an≠0 i bn≠0.

Chapter 10.2 Constant component, i.e. c0=0.5.
The constant component, as an average value in the period T=2π sec, is c0=0.5. It does not depend on the shift phase ϕ.
Chapter 10.2.1 Trajectory F(nj1t) for n=0 and ω0=1/sec, i.e. F(0j1t).

Fig.10-2
The trajectory F(0j1) of the function f(t) of a square wave with a shift of -30°, i.e. with the parameters:
A=1-amplitude
ω0=1/sec-pulsation corresponding to the period T=2πsec≈6.28sec.
ϕ=-30°=-π/6
50%-filling
Fig.10-2a
The trajectory F(0j1t) corresponds to the trajectory F(njω0t) for n=0 and ω0=1/sec.
A stationary Z plane, where on the real axis Re Z the vector changes acc. to. the function f(t) shown in Fig.10-2b.
Fig.10-2b
Time chart of f(t) of a square wave with ϕ=-30°=-π/6
In the next subchapters, the Z plane will start rotating at speeds ω= -nω0, i.e. at speeds -1/sec,-2/sec…-8/sec. The end of the vector will draw trajectories F(njω0). From them we will read the harmonics for the nω0 pulsation.

Chapter 10.3 First harmonic  i.e. h1(t).
Chapter 10.3.1 Trajectory F(nj1t) for n=1 and ω0=1/sec, i.e. F(1j1t).

Fig.10-3
Trajectory F(1j1t) of a square wave with a shift of -30°.
Compare the drawing with the analogous Fig.8-3 from chapter 8 for an even square wave. There, the vector sc1 had a shift ϕ=0° and was presented as a complex number in the algebraic form sc1=(1/π,0) or in other words
1/π+j0. It could just as well have been the exponential form sc1=1/π*exp(j0°), where the amplitude A=1/π and the phase ϕ=0° are clearly visible. In this chapter we will use the exponential version and therefore the centroid of the trajectory in Fig. 10-3c is sc1=|1/π|*exp(-j30°). Here |1/π| this is the so-called sc1 module
You can easily switch from the exponential version to the algebraic version and vice versa:
sc1=1/π*exp(-j30°)=1/π*[cos(-30°)+jsin(-30°)]≈0.275-j0.159
The sc1 vector is the average value of the rotating vector from Fig. 10-3b in the period T=2π sec, calculated from the formula Fig. 7-2b, chapter 7.
Revenons à nos moutons, so let’s get back to the topic.
Fig.10-3a
The radius R=1 as a vector (1,0) rotates with a speed ω=-1/sec around the point (0,0) in time T=2π sec and makes 1 revolution.
Fig.10-3b
Trajectory F(1j1t)=f(t)*exp(-1j1t) as a rotating vector modulated by the function f(t). The function f(t) is the square wave of Fig. 10-2b.
The Z plane in Fig. 10-2a will start rotating at a speed of ω=-1/sec. A rotating vector F(1j1t)=f(t)*exp(-1j1t) will be created. The Z plane will make 1 revolution, but the trajectory as a rotating vector F(1j1t)=f(t)*exp(-1j1t) will only make 1 half-turn.
Fig.10-3c
The trajectory F(1j1t) as a semicircle drawn by the end of the vector in Fig. 10-3b.
During 1 rotation of the Z plane by an angle of 0…2π, all vectors are vector summed and their average in the period T=2π sec is calculated according to the formula Fig. 7-2b chapter 7. This is the vector sc1=(1/π)*exp(-j30°). The trajectory is rotated relative to that in Fig. 8-3c chapter 8 by an angle ϕ = -30°.
Note to Fig. 10-3b,c
The above animations suggest that the upper and lower parts of the trajectories are separated by a gap T=π sec. But this is only the case at the beginning at time t=0…2π sec! Later, there is no break and the movement along the trajectory is continuous.
Chapter 10.3.2 The first harmonic in the background of a square wave i.e. c0+h1(t) or in other words, the first approximation of a square wave.
The constant component c0 is the average in the period T=2π, i.e. c0=a0=0.5.
Acc. to Fig. 10-3c
sc1=|sc1|*exp(jϕ)=(1/π)*exp(-j30°)
c1=2*sc1=(2/π)*exp(-j30°) i.e. |c1|=2/π ϕ=-30°
Acc. to Fig. 8-1f, chapter 8
h1(t)=(2/π)*cos(1t-30°)≈0.637*cos(1t-30°)

Fig.10-4
S1(t)=c0+h1(t)
i.e. the first harmonic with a constant component c0=0.5 against the background of a square wave.
This is a first approximation to our square wave.

Chapter 10.4 Second harmonic or rather its absence because c2=0 –>h2(t)=0.
Section 10.4.1 Trajectory F(njω0t)  for n=2 and ω0=1/sec, i.e. F(2j1t).
The Z plane rotates at a speed of ω=-2/sec

Fig.10-5
Trajectory F(2j1t) of a square wave with a shift of -30°
Fig.10-5a
The radius R=1 as a vector (1,0) rotates with a speed ω=-2/sec around the point (0,0) and will make 2 revolutions in time T=2π sec.
Fig.10-5b
Trajectory F(2j1t)=f(t)*exp(-2j1t) as a rotating vector modulated by the function f(t).
In 2π sec, the Z plane will make 2 revolutions, but the radius R=1 will make only 1 revolution, consisting of the first revolution of 240° and the second revolution of 120° with a break of 1π sec between them.
Fig.10-5c
The trajectory of F(2j1t) as a circle drawn by the end of the vector in Fig. 10-5b.
Obviously sc2=0. Note that from just the circle, the value of sc2=0 is not obvious! After all, the circle could have been drawn, for example, 1.5 times. Fortunately, this 1 full revolution, although with a break in the middle, is visible at 10-5b.
Note
sc2=0 and therefore the harmonic for ω=2/sec does not exist.

Chapter 10.5 Third harmonic i.e. h3(t).
Chapter 10.5.1 Trajectory F(njω0t) for n=3 and ω0=1/sec i.e. F(3j1t).
The Z plane rotates at a speed of ω=-3/sec

Fig.10-6
Trajectory F(3j1t) of a square wave with a shift of -30°
Fig.10-6a
The radius R=1 as a vector (1,0) rotates at a speed of ω=-3/sec around the point (0,0) and makes 3 revolutions in time T=2π sec.
Fig.10-6b
Trajectory F(3j1t)=f(t)*exp(-3j1t) as a rotating vector modulated by the function f(t).
In time 2π sec, the Z plane will make 3 revolutions, but the radius R=1 will make only 1.5 revolutions, consisting of a first 360° revolution and a second 180° revolution with a break of 1π sec between them. Radius R=1 stays longer in the upper half-plane than in the lower one. Therefore, the average value of the vector is sc3=(0.1/3π)=1j/3π
Fig.10-6c
The trajectory of F(3j1t) as a circle drawn through the end of the vector in Fig. 10-6b.
Centroid sc3=( 0.1/3π)=1j/3π.
Chapter 10.5.2 Third harmonic against a square wave i.e. c0+h3(t).
Acc. to Fig. 10-3c
sc3=|sc3|*exp(jϕ)=(1/3π)*exp(j90°)
c1=2*sc1=(2/3π)*exp(j90°) i.e. |c1|=2/3π ϕ=90°
Acc. to Fig. 8-1f, chapter 8
h3(t)=(2/3π)*cos(3t+90°)≈-0.212*sin(3t)

Fig.10-7
S3(t)=c0+h3(t)
i.e. the third harmonic with a constant component c0=a0=0.5 against the background of a square wave.
Chapter 10.5.3 Third wave approximation  i.e. S3=c0+h1(t)+h3(t).

Fig.10-8
S3(t)=c0+h1(t)+h3(t)
The third approximation is more similar to a square wave than the first one in Fig. 10-4

Chapter 10.6 The fourth harmonic or rather its absence
because c4=0 –>h4(t)=0.
Chapter 10.6.1 Trajectory F(njω0t) for n=4 and ω0=1/sec, i.e. F(4j1t).
The Z plane rotates at a speed of ω=-4/sec

Fig.10-9
Trajectory F(4j1t) of a square wave with a shift of -30°
Fig.10-9a
The radius R=1 as a vector (1,0) rotates at a speed of ω=-4/sec around the point (0,0) and will make 4 revolutions in time T=2π sec.
Fig.10-9b
Trajectory F(4j1t)=f(t)*exp(-4j1t) as a rotating vector modulated by the function f(t).
In 2π sec the Z plane will make 4 revolutions, but the radius R=1 will make 2 full revolutions consisting of the first 480° and the second 240° with a break of 1π sec between them.
Fig.10-9c
The trajectory of F(2j1t) as a circle drawn by the end of the vector in Fig. 10-9b.
Obviously sc4=0.
Note
sc4=0 and therefore the harmonic for ω=2/sec does not exist.

Chapter 10.7 Fifth harmonic i.e. h5(t).
Chapter 10.7.1 Trajectory F(njω0t) for n=5 and ω0=1/sec, i.e. F(5j1t).
The Z plane rotates at a speed of ω=-5/sec

Fig. 10-10
Trajectory F(5j1t) of a square wave with a shift of -30°
Fig.10-10a
The radius R=1 as a vector (1,0) rotates at a speed of ω=-5/sec around the point (0,0) and will make 5 revolutions in time T=2π sec.
Fig.10-10b
Trajectory F(5j1t)=f(t)*exp(-5j1t) as a rotating vector modulated by the function f(t).
In 2π sec, the Z plane will make 5 revolutions, but the radius R=1 will make only 2.5 revolutions (900°), including the first 585° and the second 315° with a break of 1π sec between them. Radius R=1 stays longer in the lower left quadrant than in the others. Therefore, the average value of the vector is sc5=(1/5π)*exp(-j150°)
Fig.10-10c
The trajectory of F(5j1t) as a circle drawn by the end of the vector in Fig. 10-10b.
Centroid sc5=(1/5π)*exp(-j150°).
Chapter 10.7.2 Fifth harmonic against a square wave i.e. c0+h5(t).
Acc. to Fig. 10-5c
sc5=|sc5|*exp(jϕ)=(1/5π)*exp(-j150°).
c5=2*sc5=(2/5π)*exp(-j150°) i.e. |c1|=2/5π ϕ=-150°
Acc. to Fig. 8-1f, chapter 8
h5(t)=(2/5π)*cos(5t-150°)≈-0.127*cos(5t+30°)

Fig. 10-11
S5(t)=c0+h5(t)
i.e. the fifth harmonic with a constant component c0=a0=0.5 against the background of a square wave.
Chapter 10.7.3 Fifth wave approximation i.e. S5(t)=c0+h1(t)+h3(t)+h5(t).

Fig.10-12
S5(t)=c0+h1(t)+h3(t)+h5(t)
The fifth approximation is more similar to a square wave than the third in Fig. 10-8

Chapter 10.8 The sixth harmonic  or rather its absence because c6=0 –>h6(t)=0.
Section 10.8.1 Trajectory F(njω0t) for n=6 and ω0=1/sec, i.e. F(6j1t).

Fig.10-13
Trajectory F(6j1t) of a square wave with a shift of -30°
Fig.10-13a
The radius R=1 as a vector (1,0) rotates at a speed ω=-6/sec around the point (0,0) and will complete 6 revolutions in time T=2π sec.
Fig.10-13b
Trajectory F(6j1t)=f(t)*exp(-6j1t) as a rotating vector modulated by the function f(t).
In a time of 2π sec, the Z plane will make 6 revolutions, but the radius R=1 will make a full 3 revolutions consisting of the first 720° and the second 360° with a break of 1π sec between them.
Fig.10-13c
The trajectory of F(6j1t) as a circle drawn by the end of the vector in Fig. 10-13b.
Obviously sc6=0.
Note
sc6=0 and therefore the harmonic for ω=6/sec does not exist.

Chapter 10.9 The seventh harmonic i.e. h7(t).
Section 10.9.1 Trajectory F(njω0t) for n=7 and ω0=1/sec, i.e. F(7j1t).
The Z plane rotates at a speed of ω=-7/sec
The sc7 vector is so small you can barely see it. You have to imagine it.

Fig. 10-14
Trajectory F(7j1t) of a square wave with a shift of -30°
Fig.10-14a
The radius R=1 as a vector (1,0) rotates at a speed of ω=-7/sec around the point (0,0) and completes 7 revolutions in time T=2π sec.
Fig.10-14b
Trajectory F(7j1t)=f(t)*exp(-7j1t) as a rotating vector modulated by the function f(t).
In time 2π sec, the Z plane will make 7 revolutions (2520°), but the radius R=1 will make only 3.5 revolutions (1260°), including 2 and 1/3 revolutions (840°) in the first cycle and 1 and 1/6 in the second cycle rotation (420°) with a 1π sec break between them. Radius R=1 stays a little longer in the lower right quadrant than in the others. Therefore, the average value of the vector is sc7=(1/7π)*exp(-j30°)
Fig.10-10c
Trajectory F(7j1t) as a circle drawn by the end of the vector in Fig. 14b.
Centroid sc7=(1/7π)*exp(-j30°).
Chapter 10.9.2 The seventh harmonic against a square wave i.e. c0+h7(t).
Acc. to Fig. 10-14c
sc7=|sc7|*exp(jϕ)=(1/7π)*exp(-j30°).
c7=2*sc7=(2/7π)*exp(-j30°) i.e. |c7|=2/7π ϕ=-30°
Acc. to Fig. 8-1f, chapter 8
h7(t)=(2/7π)*cos(7t-30°)≈-0.127*cos(7t-30°)

Fig.10-15
S7(t)=c0+h7(t)
i.e. the seventh harmonic with a constant component c0=a0=0.5 against the background of a square wave.
Chapter 10.9.3 Seventh wave approximation i.e. S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)

Fig. 10-16
S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)
The seventh approximation is more similar to a square wave than the fifth one in Fig. 10-12

Chapter 10.10 Eighth harmonic of a square wave or rather its absence
because c8=0 –>h8(t)=0.
Chapter 10.10.1 Trajectory F(njω0t) for n=8 and ω0=1/sec, i.e. F(8j1t).

Fig.10-17
Trajectory F(8j1t) of a square wave with a shift of -30°
Fig.10-17a
The radius R=1 as a vector (1,0) rotates at a speed ω=-8/sec around the point (0,0) and will complete 8 revolutions in time T=2π sec.
Fig.10-17b
Trajectory F(8j1t)=f(t)*exp(-8j1t) as a rotating vector modulated by the function f(t).
In time 2π sec, the Z plane will make 8 revolutions, but the radius R=1 will make the full 4 revolutions only in the first stage.
Fig.10-17c
The trajectory of F(8j1t) as a circle drawn by the end of the vector in Fig. 10-17b.
Obviously sc8=0.
Note
sc8=0 and therefore the harmonic for ω=8/sec does not exist.